二维随机变量的协方差和相关系数

---

协方差

定义：cov(X，Y)=E｛［X－E(X)］［Y－E(Y)］｝称为X，Y的协方差．

计算公式：cov(X，Y)=E(XY)－E(X)E(Y)．

性质：

(1)cov(X，Y)=cov(Y，X)；

(2)若a，b为常数，则cov(aX，bY)=abcov(X，Y)；

(3)cov(X₁+X₂，Y)=cov(X₁，Y)+cov(X₂，Y)；

(4)D(X±Y)=D(X)+D(Y)±2cov(X，Y)；

(5)若X，Y相互独立，则cov(X，Y)=0．

相关系数

定义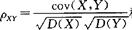：称为X，Y的相关系数．

性质：0≤|ρXY |≤1．

(1)ρXY=0，称X，Y不相关．

①若X，Y独立，则X，Y一定不相关；但不相关不一定独立；

②若(X，Y)～N(μ₁，μ₂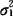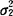，，，ρ)，则X，Y独立与X，Y不相关等价．

③若X，Y都服从(0－1)分布，则X，Y独立与X，Y不相关等价．

(2)若|ρXY|=1，则称X，Y为完全线性相关．

若Y=aX+b，则|ρXY|=1．

a＞0，ρXY=1，称为正相关．

a＜0，ρXY=－1，称为负相关．