参数的点估计

---

矩法(矩估计法)

用样本矩作为相应的总体矩的估计量．

理论根据：样本矩依概率收敛于相应的总体矩．

(1)用样本的一阶原点矩(即样本均值)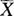作为总体的一阶原点矩(即期望)E(X)=μ的估计．即

．

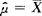(2)用样本的二阶中心矩B₂作为总体的二阶中心矩(即方差)D(X)=σ²的估计量，即．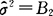

(3)用样本方差S²作为σ²的估计量，即．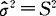

极大似然法(最大似然法)

设总体的密度函数为f(x，θ)，其中θ为要估计的参数．

极大似然法步骤如下：

(1)写出似然函数；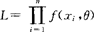

(2)求出lnL；

(3)求出；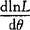

(4)解方程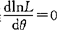，解出θ，即为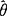(极大似然估计)．

估计量的评定标准

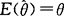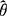(1)无偏性：如果，则称这个为θ的无偏估计量．

不难证明．

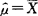是μ的无偏估计量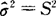，是σ²的无偏估计量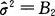．不是σ²的无偏估计量．

(2)有效性：设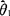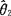，都是θ的无偏估计量，如果，

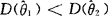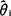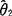则称比有效．

估计量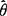的方差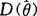有一个非零的下界，即，

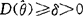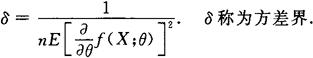
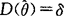f(x；θ)为总体X的密度函数．若，则称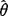为θ的达到方差界的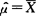无偏估计量，分别是μ，σ²的达到方差界的无偏估计量．

(3)一致性(又叫相合性)：设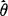是θ的一个估计量，如果对任意ε＞0，都有

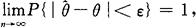
则称这个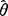为θ的一致估计量．

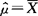是μ的一致估计量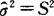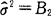．，都是σ²的一致估计量．