无穷限的广义积分的审敛法

---

定理1 设函数f(x)在区间［a，+∞)上连续，且f(x)≥0．若函数

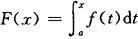
在［a，+∞)上有界，则广义积分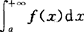收敛．

定理2(比较审敛原理) 设函数f(x)，g(x)在区间［a，+∞)上连续，如果

0≤f(x)≤g(x)(a≤x＜+∞)，

并且

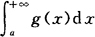
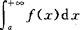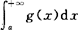收敛，则也收敛；如果发散，则也发散．

定理3(比较审敛法) 设函数f(x)在区间［a，+∞)(a＞0)上连续，且f(x)≥0．如果存在常数M＞0及p＞1，使得

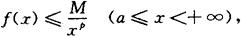
则广义积分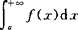收敛；

如果存在常数N＞0，使得

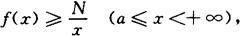
则广义积分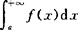发散．

定理4(极限审敛法) 设函数f(x)在区间［a，+∞)(a＞0)上连续，且f(x)≥0．如果存在常数p＞1，使得

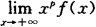
存在，则广义积分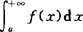收敛；

如果

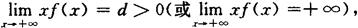
则广义积分发散．

定理5 设函数f(x)在区间［a，+∞)上连续，如果广义积分

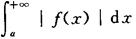
收敛，则广义积分也收敛．

绝对收敛定义 若广义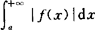收敛，则称广义积分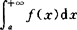绝对收敛．