欧氏空间

---

内积 设V是实数域上的线性空间，如果对V内的每一对向量α，β，都与一个确定的实数对应，这个实数记为(α，β)，并且满足下列条件：

(1)对称性：(α，β)=(β，α)；

(2)线性性：(α+β，γ)=(α，γ)+(β，γ)，(kα，β)=k(α，β)；

(3)正定性：(α，α)≥0，等号成立当且仅当α=0，则称这个实数(α，β)为向量α，β的内积，又称数量积或点积．

欧氏空间

定义了内积的实数域上的线性空间称为欧氏空间．即有了向量的度量性质的线性空间称为欧氏空间．

向量的长度

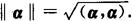
两向量间的夹角的余弦

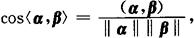
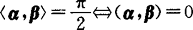，此时称两向量α，β正交．

柯西不等式

|(α，β)|≤‖α‖‖β‖．

三角不等式

‖α+β‖≤‖α‖+‖β‖．

度量矩阵 设ε₁，ε₂，…，ε_n是V_n的一组基，且有(ε_i，ε_j)=a_ij(i，j=1，2，…，n)(显然a_ij=(εi，εj)=(ε_j，ε_i)=aji，i，j=1，2，…，n)，令

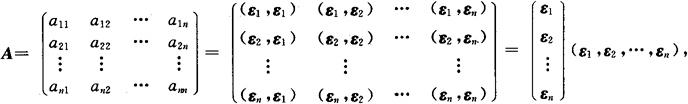
其中A=A^T，(元素的乘法是内积)则称A是V_n在基ε₁，ε₂，…，ε_n下的度量矩阵．显然度量矩阵由V_n的一组基的内积所确定．

内积的坐标表达式 设ε₁，ε₂，…，ε_n是V_n的一组基，α=x₁ε₁+x₂ε₂+…+x_nε_n，β=y₁ε₁+y₂ε₂+…+y_nε_n，则

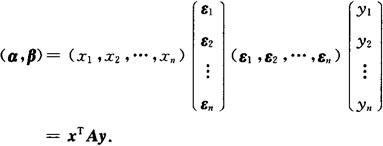
不同基下的度量矩阵是合同矩阵 设ε₁，ε₂，…，ε_n；η₁，η₂，…，η_n是V_n的两组基，其中

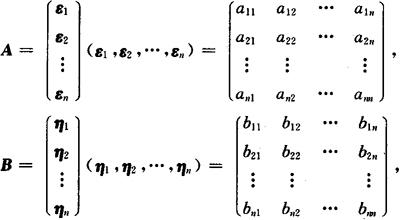
且(η₁，η₂，…，η_n)=(ε₁，ε₂，…，ε_n)C，则有B=C^TAC．

标准正交基 若ε₁，ε₂，…，ε_n是欧氏空间的一组基，且满足

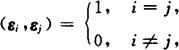
则称基ε₁，ε₂，…，ε_n为标准正交基．

标准正交基下的度量矩阵是单位矩阵 W是欧氏空间V的一个子空间，α是V的一个向量，若对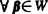，都有

(α，β)=0，

则称α与W正交，记作α⊥W．

正交子空间 设W₁，W₂是欧氏空间的两个子空间，若对于W₂，都有

(α，β)=0，

则称W₁，W₂正交，记作W₁⊥W₂．

正交补W₁，W₂是欧氏空间V的两个子空间，满足

W₁⊥W₂，W₁+W₂=V，

则称W₂为W₁的正交补(或W₁是W₂的正交补)．正交补是惟一的，记作．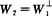

正交变换 如果欧氏空间的线性变换σ保持向量的内积不变，即对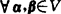，有

(σ(α)，σ(β))=(α，β)，

则称σ是正交变换．

正交变换的充分必要条件 σ是V的正交变换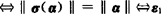，ε₂，…，ε_n是标准正交基，则σ(ε₁)，σ(ε₂)，…，σ(ε_n)也是标准正交基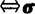在标准正交基下的对应矩阵是正交矩阵．