一元方程根的几何意义
一元方程根的几何意义yiyuan fangcheng gen dejihe yiyi
函数y=f(x)在直角坐标平面上的图象是一条曲线(图1).

图1
当曲线y=f(x)与x轴相交时,交点的横坐标就是一元方程f(x)=0的实数根.

图2
当曲线y=f(x)与x轴没有交点时,一元方程f(x)=0没有实数根.
例如,函数y=ax+b(a≠0)的图象是一条直线(图2).一元一次方程ax+b=0(a≠0)的根x=-b/a就是直线y=ax+b与x轴交点(-b/a,0)的横坐标.
又如,函数y=ax2+bx+c(a≠0)的图象是抛物线.一元二次方程ax2+bx+c=0的根就是抛物线与x轴交点的横坐标.
若判别式△=b2-4ac>0,则方程有两个实数根x12=(-b±
 )/2a,此时抛物线y=ax2+bx+c与x轴有两个交点((-b+
)/2a,此时抛物线y=ax2+bx+c与x轴有两个交点((-b+ )/2a,0)
)/2a,0)| 和 |
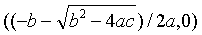
| (图3). |

图3
若判别式△=b2-4ac=0,则方程有两个实数根x1,2=-b/2a,此时抛物线y=ax2+bx+c与x轴相切于顶点(-b/2a,0)(图4).

图4
若判别式△=b2-4ac<0,则方程没有实数根,此时抛物线y=ax2+bx+c与x轴没有公共点(图5).

图5
☚ 一元二次方程的根与系数的关系 根式解 ☛
- 杏林妙法是什么意思
- 杏林庄是什么意思
- 杏枝是什么意思
- 杏枝是什么意思
- 杏枝是什么意思
- 杏枝酒是什么意思
- 杏树根是什么意思
- 杏树根是什么意思
- 杏树根是什么意思
- 杏树沟遗址是什么意思
- 杏树皮是什么意思
- 杏树皮是什么意思
- 杏核眼药是什么意思
- 杏桃散是什么意思
- 杏桃粥是什么意思
- 杏浦尊昂登是什么意思
- 杏灵丸是什么意思
- 杏熬倭瓜配色——谁也甭说谁是什么意思
- 杏胶饮是什么意思
- 杏脸桃腮是什么意思
- 杏脸香枯,色陈顑颔是什么意思
- 杏花是什么意思
- 杏花是什么意思
- 杏花是什么意思
- 杏花天是什么意思
- 杏花天是什么意思
- 杏花山是什么意思
- 杏花村是什么意思
- 杏花村是什么意思
- 杏花村汾酒是什么意思
- 杏花村汾酒酿制技艺是什么意思
- 杏花村舍是什么意思
- 杏花村馆酒旗风,水溶溶,飏残红是什么意思
- 杏花楼是什么意思
- 杏花零落燕泥香,闲立东风看夕阳。倒把凤翘搔鬓影,一双蝴蝶过东墙。是什么意思
- 杏花飞帘散余春,明月入户寻幽人。是什么意思
- 杏苏二陈丸是什么意思
- 杏苏二陈丸是什么意思
- 杏苏合剂是什么意思
- 杏苏散是什么意思
- 杏苏散是什么意思
- 杏苏散是什么意思
- 杏苏散是什么意思
- 杏苏散是什么意思
- 杏苏止咳冲剂是什么意思
- 杏苏止咳糖浆(杏苏止咳露)是什么意思
- 杏苏煎是什么意思
- 杏苏饮是什么意思
- 杏苏饮是什么意思
- 杏苏饮是什么意思
- 杏苏饮是什么意思
- 杏苏饮是什么意思
- 杏苏饮子是什么意思
- 杏苑生春是什么意思
- 杏蜜汤是什么意思
- 杏蜜汤是什么意思
- 杏蜜煎是什么意思
- 杏蜜膏是什么意思
- 杏轩医案并按是什么意思
- 杏连散是什么意思