两个平面垂直的性质定理
两个平面垂直的性质定理liangge pingmian chuizhi dexingzhi dingli
若两个平面互相垂直,则在一个平面内垂直于它们交线的直线必垂直于另一个平面.

图1
如图1,若α⊥β,α∩β=CD,AB⊂a,AB⊥CD,则AB⊥β.

图2
由上述定理还可推出:
❶若两个平面互相垂直,则经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内.
如图2,若α⊥β,P∈α,P∈a,α⊥β,则a⊂α.
❷若两个相交平面都垂直于第三个平面,则它们的交线也垂直于第三个平面.
如图3,若α⊥γ,β⊥γ,α∩β=AB,则AB⊥γ.
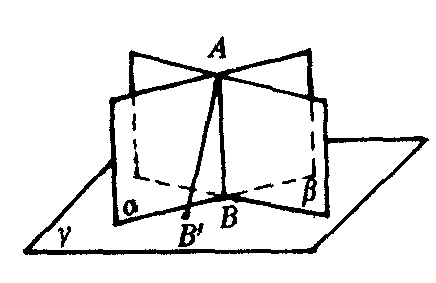
图3
证 过直线AB上任一点A,作AB′⊥γ,垂足为B′.因为A∈α,α⊥γ,根据上面的性质可知AB′⊂α.同理可证AB′⊂β.所以AB′一定与AB重合,即AB⊥γ.
❸若两个平行平面中的一个平面和第三个平面垂直,则另一个平面也和第三个平面垂直.
如图4,若α∥β,α⊥γ,则β⊥γ.
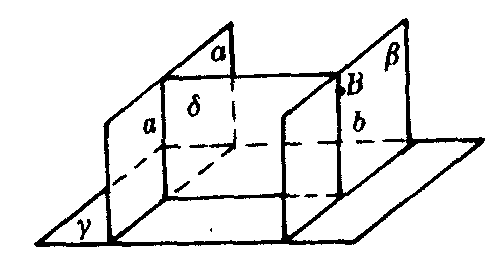
图4
证 在a内作直线a垂直于α和γ的交线.
因为α⊥γ,则α⊥γ.过α和β内任一点B作平面δ和β交于b.因为α∥β,所以a∥b.因此b⊥γ.所以β⊥γ.
以上性质主要应用在判定两条直线垂直,直线与平面垂直,或进行有关的计算方面.
☚ 两个平面垂直的判定定理 多面体 ☛
- 3. 经济法学体系是什么意思
- 3. 经济法的概念是什么意思
- 3.经营办法是什么意思
- (3)经营管理是什么意思
- 3.经费管理是什么意思
- 3.结合合同是什么意思
- 3.绘画方法是什么意思
- 3.统一经营、联产到组是什么意思
- 3.统计学是什么意思
- (3)绢制品、刺绣品是什么意思
- 3.继承是什么意思
- (3)绸、罗、锦、缎等是什么意思
- 3.综合改革实验是什么意思
- 3.综合治理阶段是什么意思
- 3.综合科技承包是什么意思
- 3. 绿化造林是什么意思
- 3.绿色证书培训是什么意思
- 3.缓岗是什么意思
- 3.缓慢发展时期是什么意思
- 3.缓慢发展阶段是什么意思
- 3.缓慢发展阶段(1966—1976年)是什么意思
- 3.缓慢增长阶段是什么意思
- 3.编目部是什么意思
- (3)编辑、出版人员是什么意思
- 3.网、带、片、点相结合综合农田防护林建设是什么意思
- 3. 罗山县是什么意思
- 3. 罗源县是什么意思
- 3.羊皮是什么意思
- 3.羊绒、羊毛、猪鬃等畜产品是什么意思
- (3)美洲是什么意思
- 3-羟-3甲基戊二酸尿症是什么意思
- 3-羟酪胺是什么意思
- 3.群众喜爱高效优质化肥是什么意思
- (3)群众工作是什么意思
- 3.群众文化教育网络是什么意思
- 3.群众渔业是什么意思
- 3 老子的治世方略和处世态度是什么意思
- 3.老马识途是什么意思
- 3.老龙头是什么意思
- (3)考务及评分是什么意思
- 3.耕作制度改革技术是什么意思
- 3.耕地占用税是什么意思
- 3.耕地占用税收入是什么意思
- 3.耙是什么意思
- 3.耳是什么意思
- 3.职业学校是什么意思
- 3.职教改革逐步深化,办学效益不断提高是什么意思
- 3.联合国专门机构是什么意思
- 3.联合育种和委托生产是什么意思
- (3)联络是什么意思
- (3)聘用、晋升、降级、调动等是什么意思
- (3)肉类是什么意思
- 3.股份联合经营型是什么意思
- 3.育种是什么意思
- 3.育苗是什么意思
- 3.育苗与造林是什么意思
- 3.育苗基地是什么意思
- (3)胶印机是什么意思
- 3. 胶州市是什么意思
- 3.脆瓜是什么意思