代数几何学
代数几何学
是用代数的方法研究几何的一门学科。代数几何学是继解析几何学之后又发展成的几何学另一分支,它研究的对象是曲面的代数曲线、空间代数曲线和代数曲面。代数几何学的兴起源于求解一般多项式方程组而开展的对这种方程组的解答所构成空间的研究,即所谓代数簇的研究。研究代数几何学的有力工具是坐标法。代数流型是代数几何学中的基本概念,也是代数几何学研究的主要对象。在笛卡尔坐标系中,Fx,y=0表示的曲线叫平面代数曲线,其中F(x,y)是关于x和y的多项式;在三维空间中,F(x,y,z)=0表示的曲面叫代数曲面,而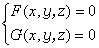 所表示的曲线叫空间代数曲线;在n维空间中,由方程组
所表示的曲线叫空间代数曲线;在n维空间中,由方程组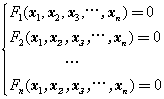
的解的集合即为代数流型。代数几何学中的定理多半是纯几何的,它所采用的坐标多建立在射影坐标系的基础上。
☚ 运筹学 黎曼几何 ☛
- 金柑是什么意思
- 金柜散是什么意思
- 金柱关之战是什么意思
- 金柱塔是什么意思
- 金柱演是什么意思
- 金柴胡是什么意思
- 金柴胡是什么意思
- 金树仁是什么意思
- 金树仁是什么意思
- 金树仁是什么意思
- 金树仁是什么意思
- 金树仁是什么意思
- 金树基是什么意思
- 金树泽是什么意思
- 金树滋是什么意思
- 金根是什么意思
- 金根是什么意思
- 金根宽是什么意思
- 金根车是什么意思
- 金桂月挂屏是什么意思
- 金桃姑娘是什么意思
- 金桃酒是什么意思
- 金桢轸是什么意思
- 金桥出口加工区是什么意思
- 金梁是什么意思
- 金梁是什么意思
- 金梁段子八吉祥帽儿是什么意思
- 金梅感冒片是什么意思
- 金梅牌兰花豆(片)是什么意思
- 金梅牌江苏老酒是什么意思
- 金梅生作品选集是什么意思
- 金梦庚是什么意思
- 金梨是什么意思
- 金森久雄是什么意思
- 金椿丸是什么意思
- 金楝散是什么意思
- 金楼子是什么意思
- 金楼子是什么意思
- 金榕八是什么意思
- 金榜是什么意思
- 金榜是什么意思
- 金榜是什么意思
- 金榜题名是什么意思
- 金榜题名是什么意思
- 金槐是什么意思
- 金槐是什么意思
- 金槐是什么意思
- 金樱丸是什么意思
- 金樱丸是什么意思
- 金樱丸是什么意思
- 金樱丸是什么意思
- 金樱丹是什么意思
- 金樱丹是什么意思
- 金樱叶是什么意思
- 金樱叶是什么意思
- 金樱叶是什么意思
- 金樱固精丸是什么意思
- 金樱子是什么意思
- 金樱子是什么意思
- 金樱子是什么意思