倒数乘除法
倒数乘除法Daoshu chengchufa
利用倒数简化运算的乘除法。某些倒数具有等于某一个整数的性质, 如:
因此,凡两因数中有一因数为5n(n为正整数)时,均可利用倒数把多位乘法转变为少位除法; 凡除数为5n(n为正整数)时,均可利用倒数把多位除法转变为少位乘法。例如:

即是把5位数乘除法化为2位数乘除法,然后再按原题据乘、除定位法定位。
此外, 由于


在一定的精确度要求下,依据与前面类似的方式,可以用3, 6, 9, 12, 15, 7, 11等简单因数的乘法代替相应的多位数除法, 求得其近似值。例如:
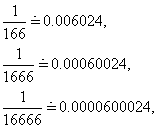
因而用6乘代替这些多位数除法分别可以得到有2位、3位、4位有效数字的近似值。
在历史上,例数乘除法始见于南宋杨辉《乘除通变本末》 (1274), 其 “单因代除”节下有:
二乘代五除, 三乘代三三三三除,四乘代二五除, 五乘代二除,
六乘代一六六六除, 七乘代一四二八除,八乘代一二五除, 九乘代一一一一除。
其“加法五术”节又有“加六代六二五除”,即16乘代625除。此后,倒数乘除法在明代王文素《新集通证古今算学宝鉴》 (1524) 中发展了两位乘数代除法。
☚ 悬珠 计算机初步 ☛
- N000356 科学王国漫步是什么意思
- N000357 100个第一的故事是什么意思
- N000359 青少年科技活动全书是什么意思
- N000367 能燃烧的“冰”是什么意思
- N000368 科学家再谈21世纪是什么意思
- N000369 运动场上学科学是什么意思
- N000371 化学·人类·社会是什么意思
- N000372 从气球到飞艇是什么意思
- N000373 儿童实验故事大全是什么意思
- N000374 小灵通是什么意思
- N000375 神秘的第六大陆是什么意思
- N000376 工交科普佳作选是什么意思
- N000377 从头到脚是什么意思
- N000379 少年儿童知识画库是什么意思
- N000381 科学启蒙百则是什么意思
- N000382 中国的超人是什么意思
- N000384 打开自然界奥秘是什么意思
- N000385 原生动物和生命科学是什么意思
- N000386 谬误集是什么意思
- N000387 人的生死之谜是什么意思
- N000389 竖鸡蛋和别的故事是什么意思
- N000390 大漠奇趣是什么意思
- N000391 改造大地的奇迹是什么意思
- N000393 森林奇观是什么意思
- N000394 鸟国之谜是什么意思
- N000396 百兽乐园趣闻是什么意思
- N000397 人体之谜是什么意思
- N000398 人与自然是什么意思
- N000399 温济泽科普文选是什么意思
- N000400 生命和微量元素是什么意思
- N000401 伟大的征服是什么意思
- N000402 小学生十万个为什么(一、二系列)是什么意思
- N000403 创造的奥秘是什么意思
- N000404 幼儿十万个为什么是什么意思
- N000406 世界奇塔莺莺塔之谜是什么意思
- N000408 百物传奇是什么意思
- N000411 神秘的蛇岛是什么意思
- N000413 人类与大自然的战斗是什么意思
- N000414 青年科技手册是什么意思
- N000416 钱三强科普著作选集是什么意思
- N000417 小金猴游地球是什么意思
- N000418 科学王国见闻是什么意思
- N000421 科学365天是什么意思
- N000422 儿童的疑问是什么意思
- N000423 告诉我为什么是什么意思
- N000424 中国的一百个世界第一是什么意思
- N000426 探险世界是什么意思
- N000427 儿童知识宝库是什么意思
- N000428 儿童百问知识画库是什么意思
- N000429 儿童知识宝库(第1辑)是什么意思
- N000430 今天的科学是什么意思
- N000434 科学的发现是什么意思
- N000435 五花八门是什么意思
- N000436 366个科学故事是什么意思
- N000437 科普作品选是什么意思
- N000438 天下之奇是什么意思
- N000439 微观探秘是什么意思
- N000440 能量博览是什么意思
- N000441 环宇搜奇是什么意思
- N000442 中学生文库(精选)·科学探索辑是什么意思