公倍数

 少广术曰：置全步及分母子，以最下分母遍乘诸分子及全步，各以其母除其子，置之于左，命通分者。又以分母遍乘诸分子及已通者，皆通而同之，并之为法。置所求步数，以全步积分乘之为实。实如法而一，得从步。
 

汉《九章算术·少广》

 少广法曰：列置全步及分母子，而副置分母自乘，以乘全步及子，各以本母除子，并之为法，以全步积分乘亩步为实，实如法而一。
 

宋·杨辉《详解九章算法·纂类》

 【评】少广术所含的通分方法比合分术有进步，使用比较小的公倍数作分母，有时可以求出最小公倍数，但尚不是完整的求最小公倍数方法。
 今有封山周栈三百二十五里。甲、乙、丙三人同绕周栈行，甲日行一百五十里，乙日行一百二十里，丙日行九十里。问周行几何日会？
 术曰：置甲、乙、丙里数，求等数为法。以周栈里数为实。实如法而得一。
 

南北朝《张丘建算经》

 【评】这里含有中国最早的最小公倍数求法。

公倍数←→公约数gōng bèi shù ← → gōng yuē shù

公倍数：能同时被几个数整除的数是这几个数的公倍数，如24是2、3、6、8、12的公倍数。
公约数：能同时整除几个数的数是这几个数的公约数，如4是8、12、16、20的公约数。

公倍数Gongbeishu

几个自然数公有的倍数，叫做这几个自然数的公倍数。例如，54是6的倍数，也是9的倍数，所以54是6与9的一个公倍数。18是6的倍数，也是9的倍数，所以18也是6与9的一个公倍数。又如，30是2的倍数，也是3的倍数还是5的倍数， 因此， 30是2, 3, 5的一个公倍数。
因为两个自然数的积是这两个自然数的公倍数，所以任何两个自然数总有公倍数。又因为一个自然数的倍数的集合是无限的， 所以几个自然数的公倍数的集合也是无限的。例如：4的倍数集合M= {0,4,8,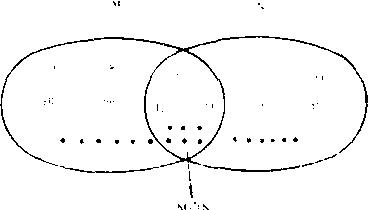12, 16, 20, 24, ……}, 6的倍数集合N ={0,6,12,18, 24, 30, 36, ……}。那么， 4与6的公倍数集合M∩N= {0, 12, 24, 36，……}也是一个无限集合。
见图示。

公倍数

common multiple