双列与点双列相关系数shuanglie yu dian shuanglie xi-angguan xishu

在双列变量中有一列为连续变量，而另一列为“二分”变量(如男生与女生、合格与不合格、三好学生与非三好学生等)或可人为地分成“二分”变量。此时可用下式计算这双列变量的相关：

式中 rpb——点双列相关系数
r_b——双列相关系数
——连续变量中P部分（如男生或合格生或答对者等）的平均值
——该变量中另一部分，即q部分（如女生或不合格生或答错者等）的平均值，q=1-p
S_x——连续变量X的标准差
Y——p的正态曲线的高度，可查正态表得到
[例] 在某班中随机抽取15名学生的数学期考成绩如下。向数学期考成绩与学生的性别是否有关？

生别	男	男	女	男	男	女	女	男	男	女	女	女	女	男	男
X	81	56	48	89	64	62	78	52	79	62	81	55	68	57	85

设男生为p、女生为q，则p=8/15=0.53、q=0.47。然后分别计男生与女生的平均分：＝(81+56+…+85)/8=70.38,＝(48+62+…+68)/7=64.86,SX=12.82，把它们代入公式得：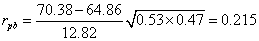

所计得的点双列相关可通过查“积差相关系数显著性临界值表”进行显著性检验。据f=15=2=13及a=0.05可知，r(₁₃)₀.₀₅＝0.514；由rpb13)₀.₀₅，故rpb无显著意义，即男、女生在学习数学上并没有明显的相关。