向量的减法
向量的减法xiangliang de jianfa
两个向量相减所得的结果仍然是一个向量,叫两个向量的差.
我们规定,第一个向量减去第二个向量,等于第一个向量加上第二个向量的相反向量.即a-b=a+(-b).这与初等代数中a-b=a+(-b)的规定是相同的.
向量的减法还可以用另一种方法来定义.即a-b的结果是一个向量x,它与所减向量b的和就是被减向量a.把这样定义得到的等式x+b=a的两边同时加上(-b).从x+b+(-b)=a+(-b)同样可以得到x=a+ (-b).
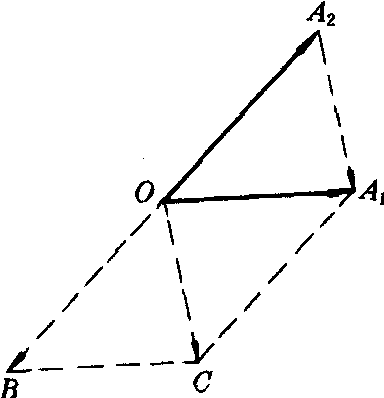
两个自由向量的起点总可以移到同一点.因此我们特别讨论一下起点相同的两个向量相减的结果,例如
 -
- ,见图
,见图 =-
=- .根据向量的加法、减法及自由向量的定义,
.根据向量的加法、减法及自由向量的定义, -
- =
= +(-
+(- )=
)= +
+ =
= =
= ,所以,起点相同的两个向量相减,结果是一个向量,其起点是所减向量的终点,终点是被减向量的终点.
,所以,起点相同的两个向量相减,结果是一个向量,其起点是所减向量的终点,终点是被减向量的终点.向量a,b与a-b的模有以下关系:
||a|-|b||≤|a-b|≤|a|+|b|
当a,b同向量时,左等号成立,当a,b反向时,右等号成立.当a,b中有零向量时,两等号同时成立.当a,b不共线时,上式的几何意义是三角形任一边小于另两边之和.大于另两边之差.
☚ 向量的和 向量的差 ☛
- 传播淫秽物品罪是什么意思
- 传播类型是什么意思
- 传播者是什么意思
- 传播者、受者和把关者是什么意思
- 传播:文化与理解是什么意思
- 传教团发起地方语言地位问题的辩论是什么意思
- 传教士与近代中国是什么意思
- 传教士到泰国传教是什么意思
- 传春散是什么意思
- 传是楼是什么意思
- 传是楼书目是什么意思
- 传昱是什么意思
- 传来取得是什么意思
- 传来证据是什么意思
- 传来证据是什么意思
- 传来证据是什么意思
- 传杰是什么意思
- 传染是什么意思
- 传染是什么意思
- 传染性单核细胞增多症是什么意思
- 传染性单核细胞增多症是什么意思
- 传染性肝炎是什么意思
- 传染性胰腺坏死病是什么意思
- 传染性角膜结膜炎是什么意思
- 传染性造血组织坏死病是什么意思
- 传染病是什么意思
- 传染病)是什么意思
- 传染病与流行病学是什么意思
- 传染病分类制度是什么意思
- 传染病医护常规手册是什么意思
- 传染病学是什么意思
- 传染病学是什么意思
- 传染病学是什么意思
- 传染病学是什么意思
- 传染病学是什么意思
- 传染病学与流行病学是什么意思
- 传染病学与流行病学是什么意思
- 传染病学及流行病学是什么意思
- 传染病护理是什么意思
- 传染病报告是什么意思
- 传染病控制措施是什么意思
- 传染病的秘密是什么意思
- 传染病监测是什么意思
- 传染病监测是什么意思
- 传染病监督管理是什么意思
- 传染病科工作质量检查提要是什么意思
- 传染病科技术管理是什么意思
- 传染病管理行政处罚是什么意思
- 传染病菌种、毒种扩散罪是什么意思
- 传染病证治从新是什么意思
- 传染病防治失职罪是什么意思
- 传染病防治法是什么意思
- 传染病防治法是什么意思
- 传染病预防是什么意思
- 传染病预防管理是什么意思
- 传染病预防管理是什么意思
- 传染链锁是什么意思
- 传檄而定是什么意思
- 传法宝记并序是什么意思
- 传法正宗记是什么意思