回归正交设计regression-orthogonal design

试验方案的结构矩阵X具有正交性的回归设计。常用的有一次回归正交设计与二次回归正交设计。
一次回归正交设计 表达试验结果的回归方程只有常数项、线性项和线性交互作用项，其回归模型为：

由于式(3)的结构矩阵X如下，它由试验方案各处理

其中各项因素均经过线性变换为-1及1两个水平编码值，除常数项的系数为1外，其余各列均符合正交条件，所以参数β的最小二乘估计b可简化为

正交性已消除了结构矩阵中各列之间的相关性，故可剔除不显著的项。
二次回归正交设计 回归模型中包括常数项、线性项、线性交互作用项及二次项的回归正交设计，回归模型为：

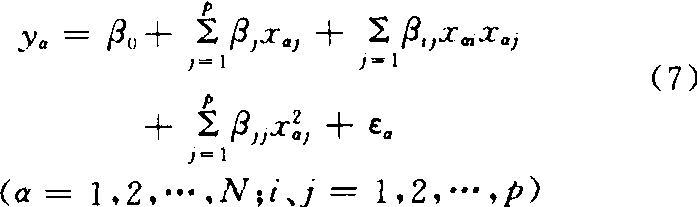
各个因素的水平数必须多于3个才可求出式(7)中的二次项。为了精确绘出二次曲线，常须进行5个水平的试验，这时处理组合数将多到无法实施，解决这个困难的方法是组合设计。组合设计各实验单元的处理内容由三部分组成：❶mo。为二水平正交表中各处理组合。
❷2p。为分布于p个因素坐标轴上距中心点距离为γ的轴点，称为星号臂。
❸m₀。各因素都取零水平的中心点。
二因素及三因素试验各处理组合在因子空间中的分布如图1、2。

图1 二因素组合设计的因子空间分布

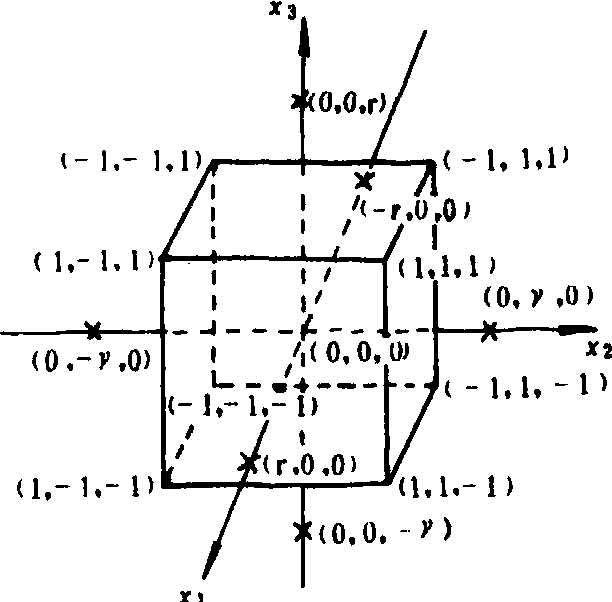
图2 三因素组合设计的因子空间分布

m₀可取不同重复次数，处理组合数目N为

N=m_o+2p+m₀ (8)

组合设计有5个水平(γ、1、0、-1、-γ)，但处理组合数目比完全实施方案少得多，从而减少过多的剩余自由度。
为了使式(7)结构矩阵符合正交条件采取了二个

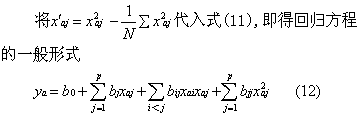
对式(11)进行显著性检验后，即可按部分处理有重复的方差分析，再在因子空间中寻优。
回归正交设计的突出优点是可以用很少的处理组合得出完全实施试验相同项数的回归模型，计算过程极为简单并已消除了回归系数之间的相关性，统计性质得到了明显改善，因此在计算机推荐施肥的多因素肥料试验中应用甚广。