坐标基底和基向量zuobiao jidi he jixiangliang

以三维欧氏空间一定点O为公共起点的三个不共面向量e₁,e₂和e₃，构成了三维欧氏空间全体向量的一个仿射坐标基底.e₁,e₂,e₃称为基向量，或称为坐标向量.
若|e₁|=|e₂|=|e₃|=1，则所构成的坐标基底称为三维欧氏空间斜角坐标基底.
若再进一步加强条件，使e₁,e₂,e₃两两相互垂直，即e₁·e₂＝e₂·e₃＝e₃·e₁＝0，则我们得到了一个三维欧氏空间直角（或正交）坐标基底.我们通常使用的就是直角坐标基底.此时基向量用i,j,k表示，并且基向量的排列顺序成右手系i×j=k,j×k=i,k×i=j.

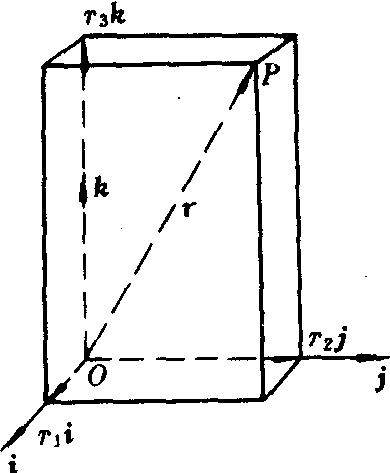
对于空间中任一以O点为始点的定向量r（如图）.若该向量关于基向量i,j,k的分解式为r=r₁i+r₂j+r₃k，则有序系数组r₁,r₂,r₃叫作该向量在此坐标基底下的坐标，记为r=(r₁,r₂,r₃).这与该向量终点
P的坐标P(r₁,r₂,r₃)是完全一致的.在此坐标基底下，基向量的坐标是i= (1,0,0),j=(0,1,0),k= (0,0,1).