垛积比类

227 垛积比类

清李善兰关于垛积术的专著。《则古昔斋算学》中的一种。4卷，约4.5万字。其内容与研究方法均属现代组合数学范畴，为早期组合数学史上的杰作。据推测约写于1853年前后。该书所列15张垛积表以贾宪三角 (扩展到 (a+b)¹²的情况) 为基础，形成一个严谨、完整的系统。且图、表、法俱全，相互配合，为任何他书所未见。给出包括一批重要定理在内的各种级数求和公式124个。还涉及一些方程，其系数最大达101，次数最高达10次。结构严谨，条理清楚，形式新颖。以中算书的传统方式讲述，无任何西方数学影响之痕。李善兰在中国传统的垛积术研究基础上所获一些相当于现代组合数学的成果均收于该书。如“三角垛有积求高开方廉隅表”和“乘方垛各廉表”实质上就是组合数学中第一种斯特林(J. Stirling,1692—1770)数和欧拉(L.Euler,1707—1783) 数。“三角自乘垛”求和公式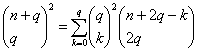
，即驰名中外的“李善兰恒等式”，自20世纪30年代起受到国际数学界的普遍关注和赞赏。

垛积比类

四卷。清李善兰 (详见《方圆阐幽》撰。这是自朱世杰《四元玉鉴》之后讨论高阶等差级数求和的最优秀的著作，也是李善兰的代表作。自序中不详撰著年月，当代中算史家李俨、钱宝琮认定其时当在1859年之后，而李迪则认为应在1853—1859年写成的。《垛积比类》为研究各类垛积问题专著，属现代组合数学之范围。李善兰自称该书是他得意杰作，在卷一中他说：“今所述，有表有图有法，分条别派，详细言之，欲令习算家知垛积之术，于《九章》外别立一帜，其说自善兰始。”全书四万五千字，图、表各占1/3，文字部分为定义、定理、演草，总共给出各类式四百余则，无一应用题。以传统方式叙述，结构严谨，条理清楚，每一卷除图外可分为四个部分： (1)表和造表法。全书共有十五张垛积表，其中基本垛表六张，支垛表七张，系数表二张，是按不同方式对贾宪三角形的推广。每张表下均给出其造法，多为递归定义。(2)解和草。全书列举了五十七个具体垛的定义式，分别与表和造表法定义的各垛相当，亦具推导和演草的性质。(3)有高（层）求积术。这是全书的中心部分，给出了各种求前n项和公式124个，其中包括一批重要定理。(4)有积求高（层）术。这为前一部分逆问题，约占全书一半，给出100个方程式及112则列方程的草式，方程次数有的高达10次，最大系数为10!。书中所有定理均由归纳或推导而得，无演绎证明，但其结果全都正确。全书四卷，各自成章，每卷都构造了一个垛积体系。卷一是朱世杰的三角垛及其派生的各支垛，并对朱世杰三角垛求和公式加以推广；卷二为乘方垛及各支垛，讨论了当p为任何正整数时，级数1+2^p+3^p+…+n^p的求和公式；卷三为三角自乘垛和各支垛，并创立了著名的“恒等式”： (f^r_p)²＝f^r_2p+ (C^p₁)²f^2r-1+ (C^p₂)²f^r-2_2P+…+(C^p_p)²f^r-p_2p。其中CIP是二项式定理系数P!/(p-i)!i!。卷四讨论的三角变垛是朱世杰的岚峰形垛以及三角再变垛、三角三变垛的求和公式。《垛积比类》以表为纲，全书的内容均建立在表的基础上，造表的方法最主要的一是改变“表根”（即初始条件），二是利用递推公式计算表内（不含最外侧两斜行）各数而得。值得注意的是“三角垛有积求高开方廉隅表”，其中各数以IkP记之，另一为“乘方垛各廉表”，各数以Lkm表示。这两表分别是两类方程的系数表，Ikp与Lkm被称为“李善兰数”，与现代组合数学中的第一种斯特灵数与欧拉数关系十分密切，李善兰通过独立研究，获得了大批成果，有些工作超过了国外的同类工作。自1867年之后的40年平均每两年出版一种垛积术著作，可见《垛积比类》影响之大。当代数学家图兰帕尔(匈牙利，1910—1976)、华罗庚(1910—1985)还为“李善兰恒等式”给出了证明。李善兰的《垛积比类》是早期组合数学的杰出著作。该书的版本主要有：《则古昔斋算学》本，有现藏北京图书馆的1867年金陵刊本和积山书局石印本，并有现藏故宫博物院的1882年江宁藩署刊本；《古今算学丛书》本，现藏北京、北大、清华、浙江、湖南各处的图书馆及中科院自然科学史研究所。