复数的三角形式fushu de sanjiao xingshi

复数z=a+bi(a,b∈R)写成z=|z|·(cosθ+isinθ)的形式，其中|z|表示复数z的模，θ是复数z的一个辐角.称z=|z|(cosθ+isinθ)为复数的三角形式.由于复数z的辐角不是唯一的，因此，把复数z表示成三角形式也不是唯一的.但是，每一个不等于零的复数有唯一的模和辐角的主值，并且可由它的模和辐角的主值唯一确定，在此意义下，可认为复数z的三角形式是唯一确定的.例如，

都是用三角形式表示的复数.
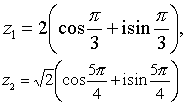
由于z=0的辐角是任意的，所以把z=0表示成三角形式时，辐角可以取任意值.
注意，z=r(cosθ-isinθ)或z=r(-cosθ+isinθ)或z=r(-cosθ-isinθ)(其中r是z的模)都不是复数z的三角形式.
复数的三角形式不仅能更形象地表示复数在平面上的位置，更重要的是计算方便，不论乘、除、乘方、开方运算，由于可以利用三角公式，计算起来都比较方便.棣莫佛定理就是利用复数的三角形式推导出来的.