复数的加法
复数的加法fushu de jiafa
两个复数相加时将实部与实部相加,所得的和做为和的实部;将虚部与虚部相加所得的和做为和的虚部.即:若z1=a1+b1i,z2=a2+b2i则z1+z2=(a1+a2)+(b1+b2)i.这就是复数的加法法则.
这样规定复数的加法自然地把实数的加法包含在内而成为复数加法的特例.(当b1=b2=0时,z1,z2是两个实数a1、a2,那么z1+z2=a1+a2)
显然两个复数的和仍然是一个复数.
复数的加法满足交换律与结合律.即
| z1+z2=z2+z1 |
| (z1+z2)+z3=z1+(z2+z3). |
这样规定复数的加法法则与向量求和的意义是一致的.因为一个复数对应一个向量,将两个复数相加的几何意义就是求这两个复数所对应的向量之和.而求向量和是按平行四边形法则进行的.例如,

 分别是复数z1=a1+b1i,z2=a2+b2i所对应的向量.如果
分别是复数z1=a1+b1i,z2=a2+b2i所对应的向量.如果
 不在一条直线上(如图),则可由平行四边形法则求得
不在一条直线上(如图),则可由平行四边形法则求得 +
+ =
= .易证明△OP2Q≌△P1PS,及四边形TP1SR是矩形.故P点坐标为(a1+a2,b1+b2).因而
.易证明△OP2Q≌△P1PS,及四边形TP1SR是矩形.故P点坐标为(a1+a2,b1+b2).因而 所对应的复数为(a1+a2)+(b1+b2)i.以上给出了复数加法的几何解释(几何意义)及用求向量和的平行四边形法则求复数的和的几何方法.即,要求两个复数z1与z2之和,可以先画出与这两个复数相对应的向量
所对应的复数为(a1+a2)+(b1+b2)i.以上给出了复数加法的几何解释(几何意义)及用求向量和的平行四边形法则求复数的和的几何方法.即,要求两个复数z1与z2之和,可以先画出与这两个复数相对应的向量
 .若
.若
 不在同一直线上,再以这两个向量为邻边作出平行四边形,其对角线向量
不在同一直线上,再以这两个向量为邻边作出平行四边形,其对角线向量 所对应的复数即为所求复数z1与z2的和.若
所对应的复数即为所求复数z1与z2的和.若 与
与 在同一直线上,则可以画一个“压扁”了的平行四边形,并据此作出对角线.
在同一直线上,则可以画一个“压扁”了的平行四边形,并据此作出对角线.两个三角形式的复数求和,一般先将它们改写成代数形式之后再相加,例如.
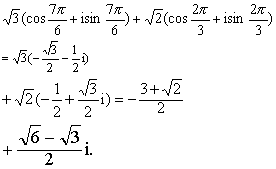
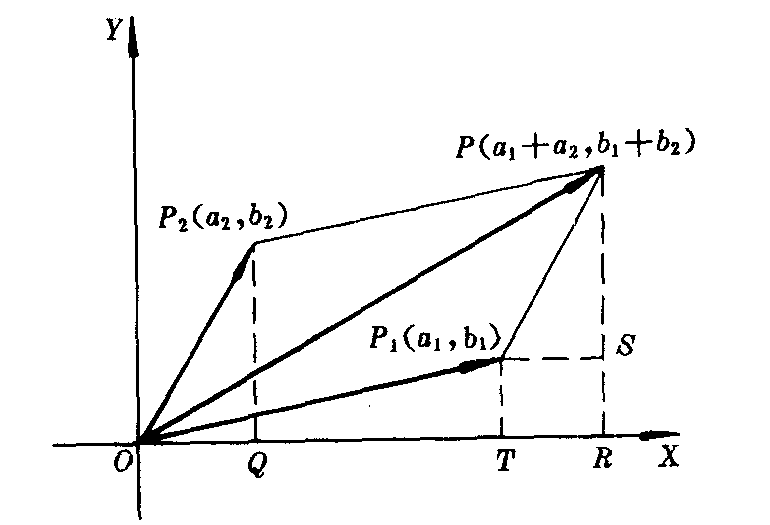
☚ 共轭虚数 复数加法法则 ☛
- 翰荃是什么意思
- 翰蔽是什么意思
- 翰蕃是什么意思
- 翰藻是什么意思
- 翰言是什么意思
- 翰逸神飞是什么意思
- 翰采是什么意思
- 翰长是什么意思
- 翰阁迟归来,传骑恨、留住难久。是什么意思
- 翰院是什么意思
- 翰院琼琚是什么意思
- 翰音是什么意思
- 翰音登于天,何可长也。是什么意思
- 翰颜是什么意思
- 翰颜氏是什么意思
- 翰风是什么意思
- 翰飞是什么意思
- 翰香館法書是什么意思
- 翰香馆法书是什么意思
- 翰馨书屋赋余是什么意思
- 翰鸟缨缴是什么意思
- 翰鹿是什么意思
- 翱是什么意思
- 翱尔钦衮噶桑波是什么意思
- 翱师是什么意思
- 翱游是什么意思
- 翱翔是什么意思
- 翱翔一万里,来去几千年。是什么意思
- 翱翔机是什么意思
- 翱翔飞行是什么意思
- 翱翔高空的大鹏是什么意思
- 翱翔,飞翔是什么意思
- 翱翥是什么意思
- 翱翱是什么意思
- 翱风亭是什么意思
- 翲是什么意思
- 翳是什么意思
- 翳云是什么意思
- 翳依是什么意思
- 翳凤骑麟是什么意思
- 翳凤骖鸾是什么意思
- 翳凤骖鸾公去,落佩倒冠吾事,是什么意思
- 翳华是什么意思
- 翳君树桃李,岁晚托深期。是什么意思
- 翳喉是什么意思
- 翳地是什么意思
- 翳垛是什么意思
- 翳塞是什么意思
- 翳夺是什么意思
- 翳如是什么意思
- 翳如丝缕是什么意思
- 翳如冰棱是什么意思
- 翳如称星是什么意思
- 翳如螺盖是什么意思
- 翳子是什么意思
- 翳子草是什么意思
- 翳子菜是什么意思
- 翳属是什么意思
- 翳庆是什么意思
- 翳徒之戎是什么意思