求三角函数的最值一般有如下三种方法.
1.三角方法:先通过三角恒等变换,化为只含有一个角的一种三角函数的式子,再依|sinx|≤1或|cosx|≤1来确定函数的最值.
2.代数方法:先通过变量代换转化为代数函数,再选用配方法、不等式法、判别式法、单调性法等求解,注意先确定换元后函数定义域.
3.解析法:将三角函数与坐标定义联系起来运用解析的知识来求其最值,这时,点线之距离公式,直线方程等都有用武之地.
三角函数的最值有如下几种常见类型.
1.y=asinx+b设t=sinx化为一次函数y=at+b在闭区间[—1,1]上的最值求解.
2.y=asin2x+bsinx+c设t=sinx化为二次函数y=at2+bt+c在闭区间[—1,1]上的最值求解.
3.y=asinx+bcosx引入辅助角φ(tanφ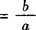 )化为
)化为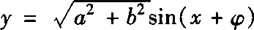 求解.
求解.
4.y=asinxcosx+b(sinx±cosx)令t=sinx±cosx化为二次函数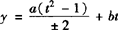 t在闭区间
t在闭区间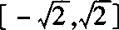 上求解.
上求解.
5.y=atanx+bcotx设t=tanx化为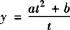 用判别式法求解.
用判别式法求解.
6. 可转化为sin(x+φ)=f(y)的形式.
可转化为sin(x+φ)=f(y)的形式.
再根据正弦函数的有界性求解,特别地也可利用数形结合转化为解析的知识求解.
例1 当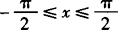 时,函数f(x)=
时,函数f(x)=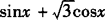 的( )
的( )
A.最大值是1,最小值是—1.
B.最大值是1,最小值是—1/2.
C.最大小值是2,最小值是—2.
D.最大值是2,最小值是—1.
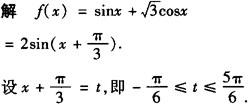
由y=sint,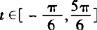 的图象知:
的图象知: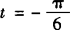 时,sint有最小值—1/2,f(x)有最小值—1;
时,sint有最小值—1/2,f(x)有最小值—1;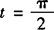 时sint有最大值1,f(x)有最大值2,故选D.
时sint有最大值1,f(x)有最大值2,故选D.
例2 求函数y=(1+sinx)(1+cosx)的最大值.
解 y=(1+sinx)(1+cosx)
=1+sinx+cosx+sinxcosx.
设t=sinx+cosx,(由三角函数的有界性知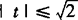 )
)
则sinxcosx=1/2(t2—1),即得y=1/2(t+1)2.
∴当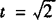 时,
时,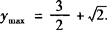 .
.
评析 对于解含有sinx+cosx和sinx·cosx的函数的最值问题,我们一般用此法求解.
例3 求函数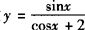 的最大值和最小值.
的最大值和最小值.
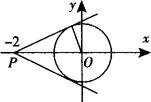
解 解法一:函数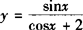 的几何意义为两点P(—2,0),Q(cosx,sinx)连线的斜率k,而Q点的轨迹为单位圆,由图可知
的几何意义为两点P(—2,0),Q(cosx,sinx)连线的斜率k,而Q点的轨迹为单位圆,由图可知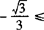
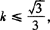 ,∴
,∴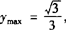 ,
,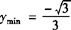 .
.
解法二:上述函数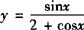 的最值问题,可令
的最值问题,可令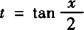 (t∈R),
(t∈R),
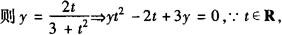
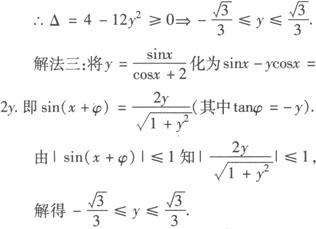
- 断钗重合;缺月再圆是什么意思
- 断钱如断血是什么意思
- 断链条𱮏狲是什么意思
- 断锦是什么意思
- 断键电荷是什么意思
- 断镭是什么意思
- 断长继短是什么意思
- 断长续短是什么意思
- 断长补短是什么意思
- 断门刀是什么意思
- 断门枪是什么意思
- 断门路是什么意思
- 断间是什么意思
- 断阶着水是什么意思
- 断限是什么意思
- 断除是什么意思
- 断陷盆地是什么意思
- 断雁是什么意思
- 断雁孤鸿是什么意思
- 断雁沉鱼是什么意思
- 断雁高仍急,寒溪晓更清。是什么意思
- 断雍门之树案是什么意思
- 断雨是什么意思
- 断雨残云是什么意思
- 断雨残云千里隔,琼枝璧月四时新。是什么意思
- 断雨残云无意绪,寂寞朝朝暮暮是什么意思
- 断雨零云是什么意思
- 断雨零风是什么意思
- 断雾是什么意思
- 断霓是什么意思
- 断霞倦鹊,未晚先争宿。是什么意思
- 断霞明似日,急雨过如风。是什么意思
- 断霞明空暮江白,密阴藏雨秋原香。是什么意思
- 断霞鱼尾画金焦,残阳鸦背分吴楚。是什么意思
- 断霭是什么意思
- 断面是什么意思
- 断面动作是什么意思
- 断面图是什么意思
- 断面教学法是什么意思
- 断面特征是什么意思
- 断面解剖与mri ct ect对照图谱是什么意思
- 断面解剖学是什么意思
- 断面计数是什么意思
- 断鞅是什么意思
- 断音是什么意思
- 断音记号是什么意思
- 断顿是什么意思
- 断顿儿是什么意思
- 断顿;断饨是什么意思
- 断颈是什么意思
- 断颈缠头是什么意思
- 断食综合疗法是什么意思
- 断首是什么意思
- 断香是什么意思
- 断香火是什么意思
- 断香烟是什么意思
- 断香铭 - 〔明〕钟惺是什么意思
- 断香零玉是什么意思
- 断马剑是什么意思
- 断骨是什么意思