三角形内角和定理的两个推论

---

推论1：三角形的一个外角等于和它不相邻的两个内角的和．

推论2：三角形的一个外角大于任何一个和它不相邻的内角．

例1 已知，如图，AE平分∠BAC，AD=AC，求证：∠C>∠B．

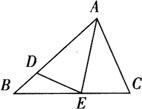
证明 在△ADE与△ACE中，

∵AE平分∠BAC，

∴∠DAE=∠CAE．

∵AD=AC，AE=AE，

∴△ADE≌△ACE(SAS)，

∴∠C=∠ADE．

∵∠ADE为△BDE的外角，

∴∠ADE>∠B(三角形的外角大于和它不相邻的任一内角)，

∴∠C>∠B．

例2 如图，已知：在△ABC中，∠ABC的平分线与∠ACB的外角平分线交于点D．求证：∠A=2∠D．

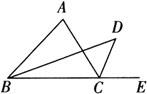
证明 ∵BD、CD分别是∠ABC与∠ACE的平分线，

又∵∠ACE是△ABC的外角．

∴∠A=∠ACE－∠ABC．

同理∠D=∠DCE－∠DBC．

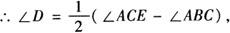
即∠A=2∠D．

[解析] 1．涉及到三角形的一个外角与和它不相邻的两个内角，这三个角中，只要知道了其中的两个角的度数，就可以求出第三个角的度数．三角形的外角，往往总隐含在图形中，在已知条件中没有明确说明，所以在应用过程中，关键是通过审图，从图形中挖出隐含条件．如果涉及到求角的度数或证明角度之间的等量关系，则应联想到三角形内角和定理的推论1．

2．凡涉及到证明有关角的不等关系，则应联想到应用三角形内角和定理的推论2．