左导数和右导数zuodaoshu he youdaoshu

设函数f (x)在点x₀的某个右邻域 [x₀,x₀+ δ)上有定义，若极限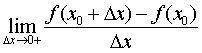存在，则称这极限值为函数f (x)在点x₀的右导数，并记作f′+ (x₀)。
设函数f (x)在点x 0的某个左邻域(x₀-δ,x₀]上有定义，若极限 存在，则称这极限值为f (x)在点x₀的左导数，并记作f′ - (x₀)。
若函数f (x)在点x₀的某个邻域内有定义，则f′ (x₀)存在的充分必要条件是，f′ +(x₀)与f′ (x₀)都存在且f′+ (x₀) =f ′ - (x₀)
注意： f′- (x₀)与f ′ (x_0-0)是有区别的。前者是函数f (x)在点x₀处的左导数，后者是f (x)的导函数f′ (x)在点x₀处的左极限。两者之一存在，不能保证另一个存在；但两者都存在时必相等。对于f′+ (x₀)与f ′ (x₀₊₀)，也有同样的结果。