不定积分

---

8．1．1 不定积分法则

∫f′(x)dx=f(x)+c，∫f″(x)dx=f′(x)+c

∫〔af(x)±bg(x)±…〕dx=a∫f(x)dx±b∫g(x)dx±…(a，b，…为常数)(线性运算)

∫f(x)dx=∫f〔φ(t)〕φ′(t)dt(变量替换)

∫f′〔φ(x)〕d(φ(x)〕=f〔φ(x)〕+C(配元积分)

∫uv′dx=uv－∫u′vdx(分部积分)

8．1．2 常见变量替换

被积函数含者，设x=asint；被积函数含者，设x==atgt；被积函数含者。设x=asect。

∫R(cosx，sinx)dx，R( )表示有理函数，设

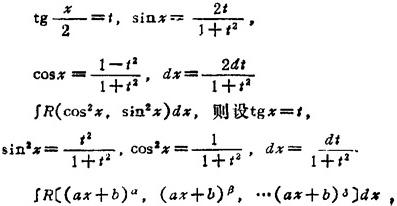
式中α，β，…，δ为分数，若分母的最小公倍为m，则设。

8．1．3 基本不定积分表

见表1．1－12。

表1．1－12 基本不定积分表(表中略去积分常数)