微分在近似计算上的应用
微分在近似计算上的应用weffen zai jinsi jisuan shangde yingyong
设f (x)是可微函数. 由于当|△x|很小时,函数的改变量与微分之差| △y-dy|比|△x|小得多,而dy又比△y容易计算,所以用dy近似代替△y是有实际意义的.
可用微分解决以下两类近似计算问题:
❶利用公式
△y =f(x0 +△x)-f(x0)≈f′(x0)△x
计算函数改变量的近似值.❷利用公式
f (x0 +△x)≈f(x0)+f′ (x0)△x
或
f(x)≈f(x0)+f′ (x0) (x -x0) (1)
计算函数值的近似值.用微分作上述的近似计算,首先要根据问题的需要确定函数f (x);然后恰当地选择x0与△x的值,使得f (x0),f ′ (x0)容易计算,且|△x|尽可能小.
例 求
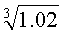 的近似值.
的近似值.解 可取
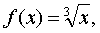 x0= 1,△x= 0. 02. 于是
x0= 1,△x= 0. 02. 于是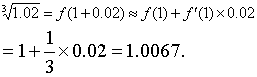
f(x) ≈f(0)+f′ (0)x (2)
当|x|充分小时,可由式(2)推出几个常用的近似公式,如sinx ≈x,tgx ≈ x,1n (1 +x) ≈x
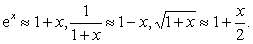
☚ 微分基本公式表 费尔马定理 ☛
- 须少是什么意思
- 须少款。是什么意思
- 须尖儿是什么意思
- 须尤其是什么意思
- 须庄是什么意思
- 须弥是什么意思
- 须弥二佛是什么意思
- 须弥入芥子是什么意思
- 须弥山是什么意思
- 须弥山石窟是什么意思
- 须弥山石窟弥勒像是什么意思
- 须弥山石窟志是什么意思
- 须弥山石窟造像是什么意思
- 须弥座是什么意思
- 须弥福寿之庙是什么意思
- 须弥福寿庙是什么意思
- 须弥福寿庙碑记是什么意思
- 须弥纳芥是什么意思
- 须弥芥子是什么意思
- 须弥藏芥是什么意思
- 须弥雪亭是什么意思
- 须弥黍米是什么意思
- 须强如是什么意思
- 须当是什么意思
- 须当归是什么意思
- 须当酒色气财捐,到如今,有甚尽。是什么意思
- 须待是什么意思
- 须得是什么意思
- 须得海之战是什么意思
- 须微是什么意思
- 须快展、亨衢阔步。是什么意思
- 须念东人年纪小(打聊目一)薛慰娘是什么意思
- 须恺是什么意思
- 须拚醉,回首夕阳流水,碧草如茵。是什么意思
- 须捷是什么意思
- 须摩堤是什么意思
- 须摩提是什么意思
- 须摩提女缘品图是什么意思
- 须摩提女缘品图壁画是什么意思
- 须摩题是什么意思
- 须教自我胸中出,切忌随人脚后行是什么意思
- 须文答剌是什么意思
- 须文达那是什么意思
- 须文那是什么意思
- 须时是什么意思
- 须明是什么意思
- 须是是什么意思
- 须是今日格一件,明日又格一件,积习既多,然后脱然自有贯通处。是什么意思
- 须是早。是什么意思
- 须是松根白茯苓。是什么意思
- 须是知得了,方能乐得,故人力行先须要知。是什么意思
- 须是骨头里挣出来的钱才做得肉是什么意思
- 须曼华馆是什么意思
- 须曼那是什么意思
- 须有凌云志是什么意思
- 须末是什么意思
- 须末那是什么意思
- 须枝是什么意思
- 须栈是什么意思
- 须根是什么意思