微积分基本公式weijifen ji b e n gongshi

若函数f (x)在区间 [a,b]上连续，且F (x)是f (x)的一个原函数，则

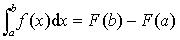
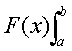F (b) -F (a)通常也用来表示，于是公式又可写成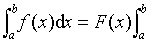

这个公式称为微积分基本公式，它是由I.牛顿、G. W.莱布尼兹发现的，因此，也称为牛顿一莱布尼兹公式.
这个公式表明，要计算只须求出f (x)的任何一个原函数F (x)，再算出f (x)在积分区间两端的函数值之差即可.
例 求
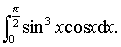
解 由于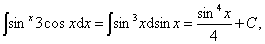所以，由牛顿-莱布尼兹公式，有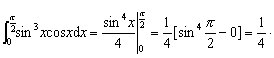
在牛顿-莱布尼兹公式建立以前，作为和式极限的定积分和作为微分运算逆运算的不定积分，是两个独立的概念. 计算每个定积分，都要从定义出发，根据被积函数的特征寻求特殊的计算方法，而这是很困难的. 牛顿—莱布尼兹公式给出了求连续函数的定积分的简便而统一的方法，把求定积分的问题转化为求原函数的问题，从而将定积分和不定积分紧密地联系起在一起. 由于有这种联系，才使微积分具有重大的理论和实用价值.