拉格朗日中值定理
拉格朗日中值定理lagelangri zhongzhi dingli
若函数f (z)满足条件❶在闭区间[a,b]上连续;
❷在开区间 (a,b)内可导,则在区间(a,b)内至少存在一点 c,使 得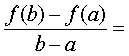 f ′ (c)或f (b)- —f (a) =f ′ (c) (6-a) (1)
f ′ (c)或f (b)- —f (a) =f ′ (c) (6-a) (1)
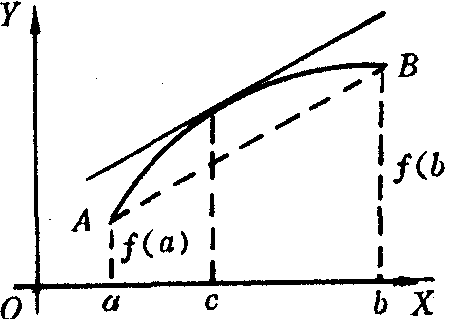
如上图所示,拉格朗日中值定理的几何意义是,若连续曲线y=f (x)的弧AB上处处具有不垂直于X轴的切线,则在这弧上至少存在一点,使曲线在该点处的切线平行于弦AB.
公式(1)称为拉格朗日公式,它有时用另一种形式表示:
f(x0 +△x)-f(x0)=f′ (x0 +θ△x) △x
其中θ是介与0与1之间的某一个数.若定理的条件不全满足,则其结论就不一定成立.然而,可以举例说明,即使定理的条件不全满足,结论仍然可能成立. 这表明,定理的条件是充分的,但不是必要的.
推论1 若函数f (x)在区间 (a,b)内有f ′ (x)≡0,则f (x) 在区间 (a,b) 内是一个常数.
推论2 若对任意x∈ (a,b)有f′(x)=g′ (x),则在区间 (d,b) 内有f(x) =g(x) +c (c为一常数).
拉格朗日中值定理精确地表述了函数在一个区间上改变量与函数在这个区间上某点导数之间的关系,而成为利用导数的局部性质研究函数整体性质的重要工具. 因此,该定理是微积分中最重要的定理之一.
罗尔定理是拉格朗日中值定理的特殊情形.
☚ 罗尔中值定理 柯西中值定理 ☛
- 徂征是什么意思
- 徂徂是什么意思
- 徂徕是什么意思
- 徂徕书院是什么意思
- 徂徕先生是什么意思
- 徂徕先生全集是什么意思
- 徂徕山是什么意思
- 徂徕山上是什么意思
- 徂徕山上红旗飘是什么意思
- 徂徕山抗日武装起义是什么意思
- 徂徕山摩崖刻石是什么意思
- 徂徕山摩崖石刻是什么意思
- 徂徕山起义纪念地是什么意思
- 徂徕山馆是什么意思
- 徂徕文集是什么意思
- 徂徕石先生文集是什么意思
- 徂徕集是什么意思
- 徂徕颂是什么意思
- 徂徠山摩崖是什么意思
- 徂徠書院是什么意思
- 徂景是什么意思
- 徂暑是什么意思
- 徂殁是什么意思
- 徂殒是什么意思
- 徂没是什么意思
- 徂泯是什么意思
- 徂秋是什么意思
- 徂背是什么意思
- 徂落是什么意思
- 徂谢是什么意思
- 徂辉是什么意思
- 徂迁是什么意思
- 徂逝是什么意思
- 徂阴是什么意思
- 徂颜是什么意思
- 徂颠是什么意思
- 徂風是什么意思
- 徂风是什么意思
- 徂魂是什么意思
- 徂龄是什么意思
- 徃是什么意思
- 径是什么意思
- 径、混流式“全可控涡”三元叶轮设计方法及是什么意思
- 径一周三是什么意思
- 径三是什么意思
- 径三三是什么意思
- 径与是什么意思
- 径乎不知。发乎不意是什么意思
- 径出重林草,池摇两岸花。是什么意思
- 径切板是什么意思
- 径向是什么意思
- 径向下锯法是什么意思
- 径向式机车转向架是什么意思
- 径向活塞泵是什么意思
- 径启者是什么意思
- 径喳是什么意思
- 径塗是什么意思
- 径奔是什么意思
- 径寸是什么意思
- 径寸珠是什么意思