无穷小量阶的比较
无穷小量阶的比较wuqiongxiaoliang jie de bifiao
设f (x),g (x)是在同一过程中的两个无穷小量,且g (x) 在这个过程中恒不为零。
❶ 若在这个过程中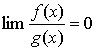 ,则称f (x)是g (x)的高阶无穷小量,记作f (x)=0 (g (x)) (在这个过程中)。
,则称f (x)是g (x)的高阶无穷小量,记作f (x)=0 (g (x)) (在这个过程中)。
❷ 若在这个过程中有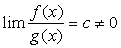 ,则称f(x),g(x) 是这个过程中的同阶无穷小量。
,则称f(x),g(x) 是这个过程中的同阶无穷小量。
若在这个过程中有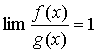 ,则称f (x),g (x)是这个过程中的等价无穷小量,记为f (x) ~g(x) (在这个过程中)。等价无穷小量显然是同阶无穷小量。
,则称f (x),g (x)是这个过程中的等价无穷小量,记为f (x) ~g(x) (在这个过程中)。等价无穷小量显然是同阶无穷小量。
❸若以x (x→0)为基本无穷小量,且f (x)与x a (a为某一正数)是同阶无穷小量(x→0),则称f (x)是关于x的a阶无穷小量。
在求两个无穷小量的比的极限时,可将其中某些无穷小量用等价的无穷小量来代替,以便简化计算。例如,
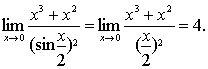
无穷小量阶的概念,反映了无穷小量趋向于零的速度,与基本无穷小量比较,无穷小量的阶越高,它趋向于零的速度就越快。
☚ 无穷小量的运算 函数在一点连续 ☛
- 钠长石辉绿岩是什么意思
- 钠长纤闪伟晶岩是什么意思
- 钠长英板岩是什么意思
- 钠长角闪辉绿岩是什么意思
- 钠长钠闪微岗岩是什么意思
- 钠闪微正长岩是什么意思
- 钠闪橄岗岩是什么意思
- 钠闪正长细晶岩是什么意思
- 钠闪石是什么意思
- 钠闪碱流岩是什么意思
- 钠闪花岗岩是什么意思
- 钠闪黑云细晶岩是什么意思
- 钠霓霞正长斑岩是什么意思
- 钠霞正长岩是什么意思
- 钠黝帘石(糟化石)是什么意思
- 钠-钾泵是什么意思
- 钡中毒是什么意思
- 钡灌肠检查是什么意思
- 钢是什么意思
- 钢是什么意思
- 钢是什么意思
- 钢是什么意思
- 钢是什么意思
- 钢—混凝土组合梁设计原理是什么意思
- 钢与混凝土组合结构设计施工手册是什么意思
- 钢丝是什么意思
- 钢丝是什么意思
- 钢丝是什么意思
- 钢丝绳是什么意思
- 钢丝绳是什么意思
- 钢丝绳的使用与维护是什么意思
- 钢丝网板条是什么意思
- 钢丝钳是什么意思
- 钢中大型非金属夹杂物是什么意思
- 钢中贝氏体是什么意思
- 钢中非金属夹杂物图谱是什么意思
- 钢中非金属夹杂物鉴别是什么意思
- 钢刀模冲切是什么意思
- 钢分类是什么意思
- 钢制压力容器是什么意思
- 钢制压力容器焊接工艺是什么意思
- 钢制及铝合金制框架(JIS A4706)是什么意思
- 钢加热学是什么意思
- 钢包是什么意思
- 钢化玻璃是什么意思
- 钢化玻璃是什么意思
- 钢卷尺是什么意思
- 钢压杆的承载力是什么意思
- 钢及其热处理曲线手册是什么意思
- 钢号是什么意思
- 钢和合金中的稀土元素是什么意思
- 钢和钼中夹杂物的鉴定是什么意思
- 钢和铁、镍基合金的物理化学相分析是什么意思
- 钢哈拉特比克是什么意思
- 钢城新余是什么意思
- 钢夫的故事是什么意思
- 钢带是什么意思
- 钢弦式传感器及其应用是什么意思
- 钢手桥是什么意思
- 钢打铁铸是什么意思