无穷级数wuqiong jishu

将数列 {u_n} 的项依次用加号连接起来，即

u₁ +u₂ +…+u_n +…　(1)

或简写为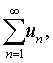，称为数项级数或无穷级数。其中u n称为级数 (1)的通项。级数 (1)的前n项和S_n＝u₁+u₂+…+u n称为级数(1)的部分和。若级数(1)的部分和数列{S_n)收敛，设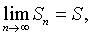则称级数 (1)收敛，并称S是级数 (1)的和，记作若部分和数列 {S_n) 不存在极限，则称级数 (1)发散。
当级数 (1)收敛于S时，称R_n＝S-S_n为级数(1) 的第n个余项，且
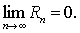
几何级数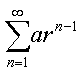与广义调和级数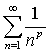等是最常见的级数。级数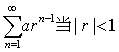时收敛，其和为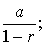当|r|≥1时发散。级数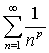当p>1时收敛；当p≤ 1时发散。
无穷级数有如下主要性质：
❶ 若级数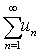收敛，则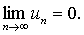

❷ 若级数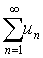收敛，C为任一常数，则级数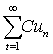也收敛，且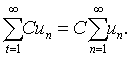

❸若级数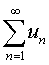与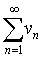都收敛，则级数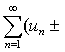v_n) 也收敛，且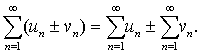

❹ 去掉、增加或改变级数的有限项，并不改变级数的收敛或发散的性质。

❺ 对收敛级数的项任意加括号 （但不改变其次序） 后构成的新级数仍然收敛，且其和不变。
无穷级数理论是数学分析的重要组成部分。无穷级数理论主要用于❶表示函数；
❷近似计算函数值、积分值和微分方程的解。