中心极限定理

---

法国数学家德·莫威尔(De Moivre)于1733年首次说明。

直到1901年由李雅普诺夫(Liapounov)在一般条件下推导出此定理。1920年卜里耶(Polya)第一次命名为中心极限定理，并为数理统计学界采用。

设独立随机变量序列x₁，x₂，…x_n，…的均值Ex₁和方差Dx₁都存在，令：

若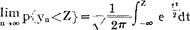成立，则我们称｛x₁｝服从中心极限定理。

如果费勒条件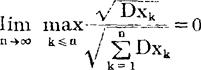满足时，中心极限定理成立的条件是所谓的林德贝格条件：对任何t＞0，成立

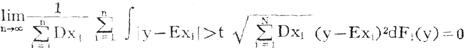
中心极限定理说明许多随机变量的分布是正态或近似正态的，这就可简化统计推断中许多统计量的分布问题。

它是数理统计中的重要工具之一。