曲线运动quxian yundong

质点的运动轨迹为 一曲线的运动。根据运动叠加原理，可以把质点的平面曲线运动看作是二个相互垂直的分运动叠加的结果，一般用矢量方法处理最方便。如图，设质点在平面上运动的轨迹为曲线AB，用位置矢量rA和rB表示质点在A点和B点的位置。在时间间隔△t内，质点由A点到B点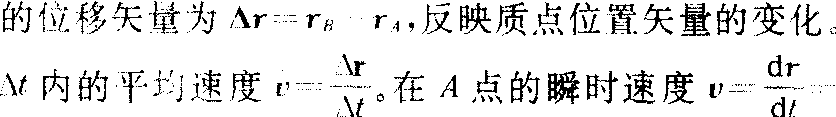vxi+vyj，它描述质点位置矢量的瞬时变化率。A点速度的方向是沿该点曲线的切线方向，并指向质点前进的一侧。由于曲线上各点的切线方向不同，质点运动的速度方向在不断地改变，所以曲线运动必定是变速运动。某点瞬时加速度a=dv/_dt=ax_i+ayj，式中ax=_dv_x/dt,ay=d^vy/_dt。它既反映了速度数值的变化，又反映了速度方向的变化。质点做曲线运动的加速度方向一般与该时刻的速度方向不相一致，加速度总是指向轨道曲线凹的一边。如果速率是增大的，则a与v成锐角；如果速率是减小的，则a与v成钝角；如果速率不变，则a与v成直角。

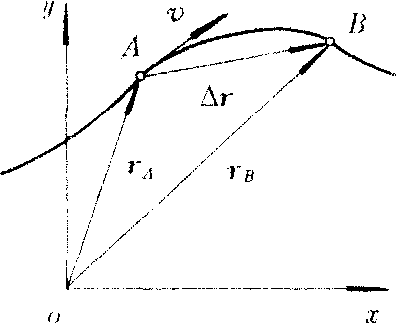
质点做曲线运动的条件是：它受到的合外力的方向跟速度的方向不在同 一直线上，而是成一角度。例如水平抛出的石子，大炮斜向上射出的炮弹，因所受重力的方向与速度方向不在同一直线上，所以石子和炮弹作曲线运动。一般曲线运动的特征是：质点运动速度的方向和大小同时改变，既有法向加速度a_n又有切向加速度aτ，即a=a_nn+a_ττ。n和τ分别是曲线上某点的法线方向单位矢量和切线方向单位矢量。

曲线运动

curvilinear motion