柯布—道格拉斯生产函数Cobb-Douglas Production Function

现代西方经济学中流行的生产函数理论之一。生产函数表示生产要素(劳动、资本、土地等)的某种组合同它所产出的最大产量之间的依存关系。就产出量与生产规模之间的关系来看，其生产函数一般有三种不同类型：当不改变各生产要素配合比，而使它们比如说都增加一倍时，如果产出量相应增加一倍，则可认为这种函数具有收益不随生产规模而改变的特点；反之，如各种生产要素都增加一倍时，产出量的增加大于或小于一倍，则分别被称为收益随生产规模递增或递减。柯布—道格拉斯生产函数具有上述第一种函数的特点。最初是美国数学家柯布和经济学家道格拉斯共同探讨投入和产出的关系时创造的生产函数，是生产函数一般形式的改进，引入了技术资源这一因素。函数表达式为：Q=AL^aK^1-a。其中，Q代表产出量，L代表劳动投入量，K代表资本投入量，A、a为常数，其中，a是小于1的正数。

柯布—道格拉斯生产函数

现代西方经济学中流行的生产函数理论之一。生产函数表示生产要素 (劳动、资本、土地等)的某种组合同它所产出的最大产量之间的依存关系。就产出量与生产规模之间的关系来看，其生产函数一般可以有三种不同类型： 当不改变各生产要素配合比，而使它们，比如说都增加一倍时，如果产出量相应地增加一倍，则可认为这种函数具有这样的特点，即收益不随生产规模而改变；反之，如各种生产要素都增加一倍时，产出量的增加大于或小于一倍，则分别被称为收益随生产规模递增或递减。柯布一道格拉斯生产函数具有上述第一种函数的特点。美国经济学家柯布，特别是道格拉斯根据有关历史统计资料估算认为，美国20世纪以来的总量生产函数具有这样的形式：

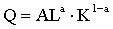
式中，Q代表产出量，L代表劳动投入量，K代表资本投入量，A、a为常数，其中，a是小于1的正数。

柯布—道格拉斯生产函数CobbDouglas production function

现代西方经济学中流行的生产函数理论之一。生产函数表示生产要素(劳动、资本、土地等)的某种组合同它所产出的最大产量之间的依存关系。就产出量与生产规模之间的关系来看，其生产函数一般可以有三种不同类型：当不改变各生产要素配合比，而使它们，比如说都增加一倍时，如果产出量相应地增加一倍，则可认为这种函数具有这样的特点，即收益不随生产规模而改变；反之，如各种生产要素都增加一倍时，产出量的增加大于或小于一倍，则分别被称为收益随生产规模递增或递减。柯布—道格拉斯生产函数具有上述第一种函数的特点。美国经济学家柯布，特别是道格拉斯根据有关历史统计资料估算认为，美国 20世纪以来的总量生产函数具有这样的形式：

Q=AL^a·K^1-a

式中，Q代表产出量，L代表劳动投入量，K代表资本投入量，A、a为常数，其中，a是小于1的正数。

柯布—道格拉斯生产函数Cobb-Douglass production function

由美国经济学家柯布和道格拉斯于本世纪30年代初建立，其具体形式为Q=A ·L^a·K^b，其中Q代表产出，A、a、b均为常数。其中A为效率参数，a为产量对于劳动投入的弹性，b为产量对于资本投入的弹性，L和K分别为劳动和资本投入。该函数是a+b次齐次生产函数，因为当L和K分别乘以某一常数k时，产出Q将增长K^(a+b)倍，即有Q′=A· kL^a· k K^b＝k^(a+b)(A ·L^a·K^b)。由于柯布和道格拉斯在建立生产函数时假定a+b=1，故该函数实际上成为线性齐次生产函数，它显示了规模收益不变的特性。当a+b大于或小于1时，该函数将分别显示规模收益递增和规模收益递减的特性。
与柯布—道格拉斯函数相联系的等产量曲线，呈现为一条凸向原点的圆滑曲线。对于线性齐次的柯布—道格拉斯生产函数，可以推导出几个重要性质： (1) 资本与劳动的平均和边际产品唯一地成为资本与劳动比例的函数； (2) 尤勒定理 ( Euler′s Theorem) 成立； (3) 如果每一种投入根据其边际产品支付报酬，那么函数中的两个指数a和b将实际上测量总产品分别归于劳动和资本的份额。

柯布—道格拉斯生产函数

在分析美国1899—1922年间经济统计资料基础上得出的一个美国的生产函数，以其发明者而得名。它的基本含义可用公式表示： Q=kLαC1-α(Q表示产量，L表示劳动投入量，C表示资本投入量，k表示一正常数，α表示小于1的正数)，即产量取决于劳动和资本的某一组合。它的形成有一个过程。按照熊彼特的考证，本世纪初瑞典经济学家威克塞尔最先设想出社会生产函数公式： P=aαbβ(P表示产量，a、b均表示生产要素，α+β=1)。1934年，美国经济学家道格拉斯发表了他知名著作《工资理论》，邀请长于数学的友人柯布为他的理论设计公式。他们在威克塞尔的上述公式里加了一个常数C，由此得出社会生产函数Z=CV1αV21-α(Z表示产量，C表示一常数，V1、V2表示生产要素)。尔后，他们根据历史统计资料，研究1899—1922年间美国资本和劳动这两种生产要素对产量的影响，把上述公式加以扩充，发挥和应用到美国，得出了这一时期美国的生产函数为：Q=KLαC1-α，此即柯布—道格拉斯生产函数的由来。这一公式表明： 在总产量中，工资的相对份额是α，资本收益的相对份额是1-α。根据美国统计资料，20世纪以来，α=3/4,1-α=1/4，这说明每增加劳动1%所引起的产量的增长，将三倍于每增加资本1%所引起的产量的增长。这一结论被认为与美国工资收入与资本收益之比 (3 : 1) 大体相符。