正多面体的种类zhengduomianti de zhonglei

正多面体只有五种.证明如下：
设正多面体的各个面都是正n边形，在各个顶点的棱数都是m，也就是说，每个顶点都是一个m面角的顶点(m,n都是不小于3的整数).因为正n边形的

每个内角等于

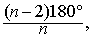
而凸m面角的面角就是正

n边形的内角，所以凸m面角的所有面角之和等于

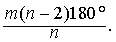
根据凸多面角的内角之和小于360°,

可知

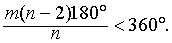
化简得

m(n-2)<2n.

因

此

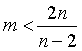
解这个不等式，得

当n=3时，m=3,4,5;
当n=4时，m=3;
当n=5时，m=3;
因为n>5时，m<3不合题意，所以n不可能大于5.
因此，只能得到关于m,n的五个数对：(3,3),(3,4),(3,5),(4,3),(5,3).这就是说，正多面体只能有五种：用正三角形做面的有正四面体、正八面体、正二十面体，在它们每个顶点的棱数分别为3,4,5；用正方形做面的只有正六面体，在它每个顶点的棱数为3；用正五边形做面的只有正十二面体，在它每个顶点的棱数为3.这五种正多面体如下图所示.

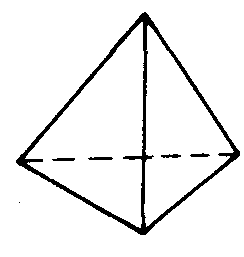
正四面体

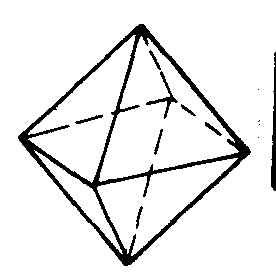
正八面体

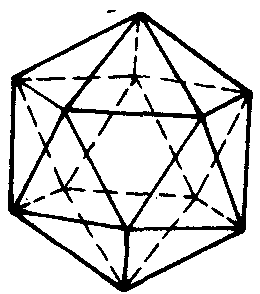
正二十面体

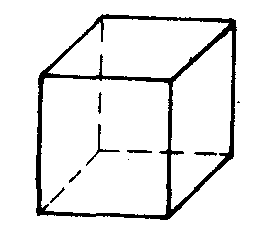
正六面体

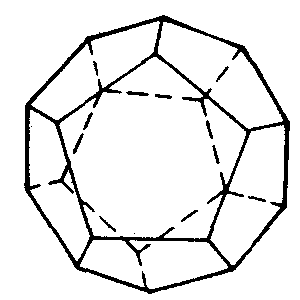
正十二面体