牛吃草Niuchicao

有三块草地，面积分别为样快。如果第一块草地可供12头牛吃4星期，第二块草地可供21头牛吃9星期，那么，第三块草地可供多少牛吃18星期？
这个看上去相当简单的问题是牛顿在他的《普通

牛吃18星期。
但是， 问题并不这样简单。由于青草在不断生长着，在不同的时间里，不同面积的草地上，新生青草的数量也不相同，上面的解法是错误的。牛顿给出了这个问题的几种解法，而他最欣赏的是下面的比例解法：
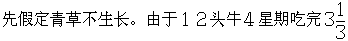
顷草地上的草，按这一比例，10顷草地可供36头牛吃4星期、或16头牛吃9星期、或8头牛吃18星期。
由于青草在生长，所以题中说10顷草地可供21头牛吃9星期。与前面假定青草不生长时的情形相比，草地面积、星期数都相同，但牛数差5头，这表明：在这9星期的前4星期里，10顷草地上生长的青草已可供16头牛吃9星期，而在这9星期的后5星期里，10顷草地上新生的青草可供5头牛吃9星期。或者说可供2.5头牛吃18个星期。
由此类推，考虑在18星期的后14星期里，10顷草地新生的青草可供多少牛吃18星期，显然有
5周：14周=2.5头牛：7头牛
也就是说， 10顷草地14星期内新生长的青草可供7头牛吃18星期。
在假定青草不长的情况下，已经算出10顷草地可供8头牛吃18星期；在考虑青草生长时，又算出10顷草地新生的青草可供7头牛吃18星期。因而，10顷草地实际上可供8+7=15头牛吃18星期。根据这个比例， 立即可以算出24顷草地可供多少牛吃18星期：
10顷：24顷=15头牛：36头牛， 即可供36头牛吃18星期。