空间两方向间的角度kongjian liaangfangxiangjian dejiaodu

两条异面射线l₁和l₂的夹角就是过空间任意一点O和它们平行且同向的射线m₁和m₂的交角θ(0<θ<π).设两条异面射线的方向余弦分别是λ₁,μ₁,γ1和λ2 ,μ2 ,γ2，又它们的夹角为θ，则cosθ=λ1λ2+μ1μ2+γ₁γ₂. 因为0<θ<π故

sinθ=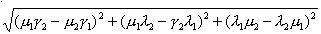

设有两点P₁ (x₁,y₁,z₁)和P₂ (x₂,y₂,z₂)，又射线OP₁和射线OP₂的交角是θ，则

以a₁ ,b₁,c₁和a₂ ,b₂ ,c₂为方向数两条直线所成的一个交角是θ，则有

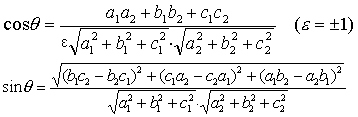
两条射线的方向余弦分别是λ₁,μ₁,γ₁和λ₂,μ₂,γ₂则它们垂直的充要条件是；λ₁λ₂+μ₁μ₂+γ₁γ₂＝0. 以a₁ ,b₁,c₁和a₂,b₂,c₂为方向数的两条直线垂直的充要条件是a₁a₂+ b₁b₂ + c₁c₂＝ 0. 两点P₁ (x₁,y₁,z₁) 和P₂(x₂ ,y₂,z₂)，则射线OP₁和OP₂垂直的充要条件是x₁x₂+y₁y₂+z₁z₂＝0.
两条射线平行且同向的充要条件是对应的方向余弦相等. 平行且反向的充要条件是对应的方向余弦互为相反数. 以a₁ ,b₁,c₁和a₂,b₂,c₂为方向数的两条直线平行的充要条件是a₁/a₂＝b₁/b₂＝c₁/c₂.