空间曲线
空间曲线kongjian quxian
若曲面F (x,y,z)=0和G (x,y,z) = 0都通过某条曲线,而且它们另外没有公共点,那么联立方程
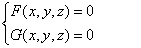
☚ 曲面的轮廓线 空间坐标变换 ☛
- 巾裹是什么意思
- 巾褐是什么意思
- 巾褠是什么意思
- 巾角垫是什么意思
- 巾角折是什么意思
- 巾角拂棋是什么意思
- 巾起是什么意思
- 巾車是什么意思
- 巾车是什么意思
- 巾车乡是什么意思
- 巾 部是什么意思
- 巾部是什么意思
- 巾针是什么意思
- 巾鞲是什么意思
- 巾鞴是什么意思
- 巾韝是什么意思
- 巾额是什么意思
- 巾𫗖是什么意思
- 巿是什么意思
- 巿部是什么意思
- 帀是什么意思
- 帀部是什么意思
- 币是什么意思
- 币之行以通农商论是什么意思
- 币仪是什么意思
- 币众财通而民乐是什么意思
- 币余之赋是什么意思
- 币值是什么意思
- 币值不变假定是什么意思
- 币值低估是什么意思
- 币值变动会计是什么意思
- 币值小的钱是什么意思
- 币值波动是什么意思
- 币值的恢复是什么意思
- 币值稳定是什么意思
- 币值重新调整是什么意思
- 币值高估是什么意思
- 币制是什么意思
- 币制则例是什么意思
- 币制实业借款是什么意思
- 币制局是什么意思
- 币制局总裁是什么意思
- 币制局督办是什么意思
- 币制改革是什么意思
- 币制改革方案的发布是什么意思
- 币制改革的失败是什么意思
- 币制改革的酝酿是什么意思
- 币制调查局是什么意思
- 币厚言甘是什么意思
- 币原坦是什么意思
- 币器是什么意思
- 币奚假于词祝是什么意思
- 币市是什么意思
- 币帛是什么意思
- 币帛之式是什么意思
- 币帛绢是什么意思
- 币材是什么意思
- 币爵是什么意思
- 币美没礼是什么意思
- 币聘是什么意思