符号检验

不管总体的分布，基于对样本数据的顺序统计量，利用数据的差异方向，把中位数作为集中优势的度量，检验两个分布是否一致的方法，称为符号检验。此法既适合于双样本检验，又适合单样本检验。其检验步骤是：1.双样本检验：设有两个总体X和Y，且x～F₁(x),y～F₂(x)，假设H₀:F₁(x)=F₂(x)。一、对两总体X和Y分别取容量相同且都是n的样本x₁…x_n1和y₁…y_n2，于是得到n对数(x₁,y₁)…(x_n,y_n)，并分别记x_i>y_i,x_i＝y_i,x_ii(1≤i≤n)的个数为n₊,n₀,n_-，且N=n_-+n₊，令r=min(n_-,n₊)。二、计算统计量：r=min(n_-,n₊)。三、查符号检验表：对于给定的显著性水平α和N，查符号检验表得临界值r_α。四、检验：如果r>r_α则拒绝原假设H₀。如果rα，则接受原假设。以上检验方法对小样本最为有效。2.单样本检验：从总体中抽取容量为n的样本x₁,x₂，…，x_n，当检验样本的中位数是否为μ₀时其步骤是：假设：μ=μ₀。一、做差数，x_i-μ₀,(i=1，…，n)，并记x_i-μ₀>0的个数为n₊,x_i-μ₀＝0的个数为n₀,x_i-μ₀<0的个数为n_-。二、计算统计量：r=min(n_-,n₊)。三、查秩和检验表：对于给定的显著性水平α和N，查秩和检验表，得临界值r_α。四、检验：如果r>r_α则拒绝原假设H₀。如果rα，则接受原假设H₀。常被应用于测验分数统计中。

符号检验sign test

非参数检验的一种。符号检验用于成对分数之差的正负方向的检验，它期望各对量数之差的正号个数与负号个数有相同的机遇，即“+”的个数等于“-”的个数n+=n_。由于实验存在着误差，n+与n-则不可能绝对相等；但一定的误差是应当允许的，不过差异不应太大。如果差异过大，不仅表明存在实验误差，而且还存在着条件误差，即实验结果有显著差异。如把正号个数以k来表示， 以n表示除零差以外的正差个数和负差个数之和，可用正整分布模型进行检验，其公式为：

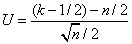
在选取一定的α显著水平下，如U>Uα/2,U值落于临界区域之内，就拒绝原假设；如U

符号检验sign test

通过比较两个相关样本每对数据之差的正负符号数目之间差异是否显著，进而比较两个样本数据之间是否有显著差异的非参数检验方法。若两个样本差异不显著，则正号与负号的数目相当。符号检验与参数检验中相关样本t检验相对应，当数据不满足t检验条件时，可采用此法进行粗略比较。符号数目差异临界值可通过查阅相应统计检验表获得。