线性概率模型
线性概率模型linear probability model
考虑线性回归模型yi=xiβ+εi,其中yi=1的概率为Pi,yi=0的概率为1-Pi。很清楚xi解释了yi=1或0的概率。让Pi=P(yi=1|xi)=F(xiβ),1-Pi=P(yi=0|xi)=1-F(xiβ)。易见E(yi|xi)=1×F(xiβ) + 0× (1 -F(xiβ))=F(xiβ)。若F(xiβ)=xiβ,则称该线性回归模型为线性概率模型。此时解释变量对被解释变量的边际影响为:
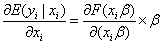
给定N个独立观测值的样本,似然函数为
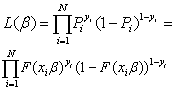
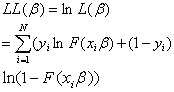
参数估计β就是最大化LL(β)的解,我们解一阶条件
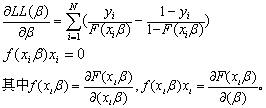
最后,海赛(Hessian)矩阵
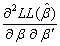 必须为负定。参数估计量的协方差阵为Var(
必须为负定。参数估计量的协方差阵为Var( )=
)=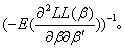
☚ 定性与限值性变量 概率变换 ☛
- 商标国际注册马德里协定联盟是什么意思
- 商标图形国际分类协定是什么意思
- 商标图样是什么意思
- 商标地区注册是什么意思
- 商标学是什么意思
- 商标异议是什么意思
- 商标异议是什么意思
- 商标异议是什么意思
- 商标异议是什么意思
- 商标异议书是什么意思
- 商标异议复审是什么意思
- 商标忠实性是什么意思
- 商标提示是什么意思
- 商标有效期限是什么意思
- 商标权是什么意思
- 商标权是什么意思
- 商标权是什么意思
- 商标权是什么意思
- 商标权是什么意思
- 商标权是什么意思
- 商标权是什么意思
- 商标权是什么意思
- 商标权是什么意思
- 商标权是什么意思
- 商标权是什么意思
- 商标权独立原则是什么意思
- 商标权的取得是什么意思
- 商标权的变更是什么意思
- 商标权转移所得是什么意思
- 商标权转让是什么意思
- 商标条款是什么意思
- 商标查询是什么意思
- 商标标签保险条款是什么意思
- 商标标识是什么意思
- 商标标识是什么意思
- 商标档案是什么意思
- 商标法是什么意思
- 商标法是什么意思
- 商标法是什么意思
- 商标法是什么意思
- 商标法是什么意思
- 商标法是什么意思
- 商标法是什么意思
- 商标法是什么意思
- 商标法是什么意思
- 商标法是什么意思
- 商标法学是什么意思
- 商标法实施细则是什么意思
- 商标法律文书是什么意思
- 商标法教程是什么意思
- 商标法条约是什么意思
- 商标法规资料选编是什么意思
- 商标注册是什么意思
- 商标注册是什么意思
- 商标注册是什么意思
- 商标注册是什么意思
- 商标注册是什么意思
- 商标注册是什么意思
- 商标注册是什么意思
- 商标注册人是什么意思