综合除法

 指用x—c去除一元多项式f(x)的一种简便的计算方法。它在计算一元多项式的值，解一元高次方程和因式分解等问题中是重要的，常用的工具。
 运用综合除法的基本要求是：①熟练掌握综合除法的简便直式(用xc去除a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n):

 得商式为b₀x^n-1+b₁x^n-2+…+b_n-1,余数为r。②懂得综合除法的算理：用待定系数法即可推得。

综合除法zonghe chufa

计算多项式f(x)除以x-a所得不完全商和余数的一种常用的比较简便的方法.
设

f(x)=a₀xⁿ+a₁x^n-1+a₂x^n-2+…+a_n-1x+a_n(a₀≠0)

除以x-a，所得的不完全商是(x)，余数是r.那么

f(x)=(x-a)(x)+r　(1)

这里(x)是x的n-1次多项式，把它记作(x)=b₀x^n-1+b₁x^n-2+b₂x^n-3+…+b_n-2x+b_n-1 (b₀≠0)
把(x)的表达式代入(1)式，经整理后可得

等式(2)是一个恒等式.由多项式恒等的定理可得

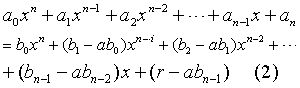
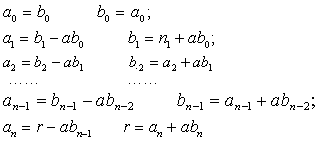
从上面右边得出的一列等式可以看到，不完全商(x)的各项系数b₀,b₁,b₂，…，b_n-1和余数r，可以从被除式f(x)的各项系数a₀,a₁,a₂，…，a_n和除式x-a中的a顺次递推出来.
为了方便，上面的计算可以列式来进行

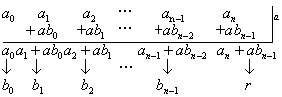
例如，求f(x)=3x⁵-14x³+7除以x-2所得的不完全商和余数，先把f(x)按x降幂排列，缺项补零、表示为完全多项式

f(x)=3x⁵+0x⁴-14x³+0x²+0x+7

由此确定各项的系数顺次是3,0,-14,0,0,7.再由x-2确定a=2，列式来计算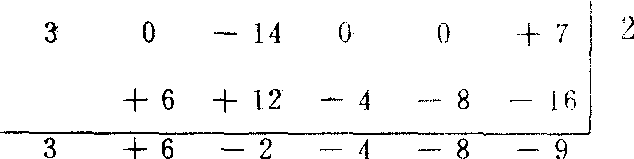

不完全商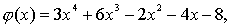余数r=-9.
象上面这样求多项式f(x)除以x-a的不完全商和余数的方法，称为综合除法.

综合除法

用x-a除多项式f(x)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a。(n≥1)的一种方法。作法如下：

式中b_n＝a_n,b_i＝a_i+b_i+₁a(i=0,1,2，…，n-1)。商式为g(x)=b_nx^n-1+b_n-1x^n-2+…+b1，余式为b0=f(a)。

综合除法

synthetic division