贝叶斯定理Bayesian Law

见“贝叶斯法则”。

贝叶斯定理Bayes Theorem

设A1,A2，…，An是一组互不相容的事件，且满足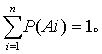假设每一个P(Ai)都是已知的，称为先验概率。如果另一事件B发生，并且假设对任何Ai,P(B|Ai)是已知的，则贝叶斯定理为：

P(Ai|B)被称为后验概率。贝叶斯定理是利用已知B发生的知识来修正Ai发生的概率。
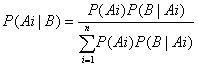
在贝叶斯定理的应用中首先要对先验概率进行假设。先验概率是主观概率。即使在决策者无任何先验信息的情况下，决策者仍可以使用贝叶斯定理，如何合理地假设先验概率是贝叶斯分析的重要问题。
贝叶斯方法和决策论的结合发展和丰富了统计推断理论，形成了统计决策理论。贝叶斯方法同时也推动了决策论和博弈论的发展，使得信息成为决策中可分析的对象。因此，贝叶斯方法成为信息经济学的重要基石。

贝叶斯定理Bayes’theorem

计算事件概率的一种方法。认为事件完成之后某个假设是正确的概率依赖于： (1)事件出现之前，该假设是正确的概率； (2)如该假设是正确的，事件可望出现的概率；(3)如其他任何假设是正确的，事件可望出现的概率。该定理的一个基本公式是P (H1/D) =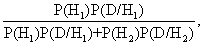其中H₁、H₂代表两个不同的假设；P (H₁)和P (H₂)代表事件出现前，H₁和H₂是正确的概率；P(H₁ /D)为事件出现后，H1是正确的概率；P (D/H₁)是在H₁正确时，事件可望出现的概率；P (D/H₂)是在H₂为正确时，事件可望出现的概率。研究表明，普通人的概率推理一般类似贝叶斯公式的预测，而在概率数值上表现出来的保守或错误，则可能由于对概率的判定或诸概率的组合不够精确所致。

贝叶斯定理Bayes's theorem

亦称“贝叶斯推理”、“贝叶斯公式”。概率计算公式之一。英国学者贝叶斯(Thomas Bayes, 1702—1763)提出。假设A₁,A₂，…，A_k构成互斥的完全事件，且P(A_i)>0(i=1,2，…，k)，则对任一事件B，且P(B)>0，有

P(A_i|B)=P(A_i)P(B|A_i)　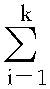P(A_i)P(B|A_i)
(i=1,2，…，k)。

其中，P(A_i)为事件A_i的先验概率，P(A_i|B)是事件A_i的后验概率。