费尔马点
费尔马点feierma dian
在三角形内部的正等角中心.若在△ABC的外边作正三角形△BCA′,△CAB′,△ABC′,则AA′,BB′,CC′三线共点.这个点叫做△ABC的正等角中心.当△ABC三个内角均小于120°时,它的正等角中心在三角形内.
以上性质分三种情况说明.
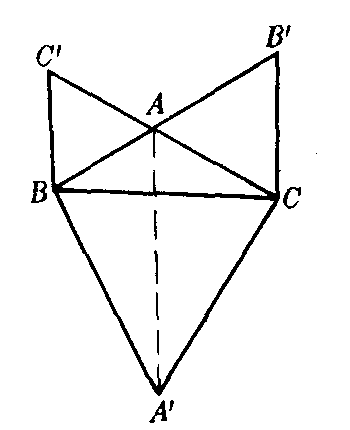
图1
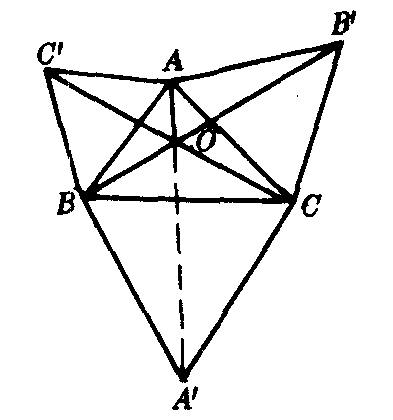
图2
❶若△ABC有一个角是120°,如图1,∠BAC=120°.显然AA′,BB′,CC′交于120°角的顶点A.
❷若△ABC各角均小于120°.如图2,设BB′,CC′交于△ABC内部一点O.连结OA,OA′,不难证明△ABB′≌△AC′C.故A与BB′,CC′等距,OA平分∠B′OC′.又∠AB′ O=∠ACO,A,B′,C,O四点共圆.∠COB′=∠CAB′=60°,∠BOC=120°,又∠BA′C=60°,所以O,B,A′,C四点共圆.由A′B=A′C,推知OA′平分∠BOC.可知A,O,A′在一条直线上.即AA′,BB′,CC′交于O点.
❸若△ABC有一个角大于120°,如图3,∠BAC> 120°.这时BB′,CC′交于△ABC外一点O.连结OA,OA′.仿
❷可证OA,OA′均平分∠BOC.所以OA,OA′重合,即AA′.BB′,CC′交于点O.
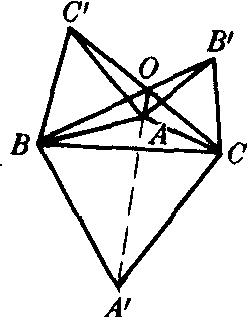
图3
☚ 证明 梅内劳斯定理 ☛
- 阻卜是什么意思
- 阻塞 梗塞 堵塞是什么意思
- 阻塞性肺气肿是什么意思
- 阻塞性脑积水是什么意思
- 阻塞性黄疸是什么意思
- 阻容耦合多级放大电路是什么意思
- 阻尼是什么意思
- 阻尼振动是什么意思
- 阻抗是什么意思
- 阻抗微分图是什么意思
- 阻抗心动图是什么意思
- 阻抗血流图是什么意思
- 阻抗血流图仪是什么意思
- 阻挠是什么意思
- 阻挡是什么意思
- 阻止是什么意思
- 阻止 阻挠 阻拦 阻遏 阻 拦是什么意思
- 阻止令是什么意思
- 阻止指令是什么意思
- 阻滞型濒死心电图是什么意思
- 阻滞性单束支传导中断是什么意思
- 阻滞性单束支传导延缓是什么意思
- 阻滞/加速性脱节现象是什么意思
- 阻燃剂化学及其应用是什么意思
- 阻碍是什么意思
- 阻碍是什么意思
- 阻碍 障碍是什么意思
- 阻碍军事行动罪是什么意思
- 阻碍军人执行职务罪是什么意思
- 阻碍国内工业建立是什么意思
- 阻碍执行公务是什么意思
- 阻碍执行公务罪是什么意思
- 阻碍执行军事职务罪是什么意思
- 阻碍解救被拐卖、绑架妇女、儿童罪是什么意思
- 阻絮凝剂(纤维分散剂)是什么意思
- 阻遏作用是什么意思
- 阿是什么意思
- 阿是什么意思
- 阿是什么意思
- 阿是什么意思
- 阿是什么意思
- 阿Q是什么意思
- 阿Q正传是什么意思
- 阿Q正传是什么意思
- 阿Q正传是什么意思
- 阿Q正传是什么意思
- 阿Q正传是什么意思
- 阿Q正传是什么意思
- 阿Q正传是什么意思
- 阿Q正传是什么意思
- 阿Q正传是什么意思
- 阿Q正传一〇八图是什么意思
- 阿Q正传创作论是什么意思
- 阿Q正传插图是什么意思
- 阿Q精神是什么意思
- 阿Q论稿是什么意思
- 阿·吉基是什么意思
- 阿·托尔斯泰是什么意思
- 阿·托尔斯泰是什么意思
- 阿·托尔斯泰是什么意思