几种常见函数的导数

---

根据导数的定义，可得出一些常见函数的导数公式：

(1)C′=0(C为常数)；

(2)(xⁿ)′=nx^n—1(n∈Q)；

(3)(sinx)′=cosx；

(4)(cosx)′=—sinx．

例1 求下列各函数的导数．

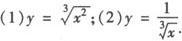
解 将根式化为幂指数形式求导．

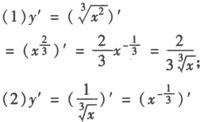
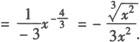
例2 求双曲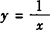线与抛物线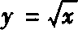在交点处的切线的夹角．

解 要求两切线的夹角，只需先求出两切线的斜率，求斜率即求导数．

函数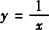的导数y′=—x^—2，函数y=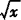的导数y′=1/2x^—1/2．

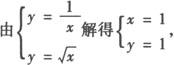
∴两曲线交点为(1，1)．

∴双曲线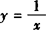在点(1，1)处的切线的斜率k₁=—1，抛物线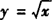在点(1，1)处的切线的斜率k₂=1/2．

设两条切线的夹角为α，

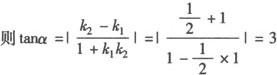
∴α=arctan3．