高阶导数gaoiie daoshu

若函数y=f (x)的导数y′ =f′ (x)在点x可导，则导数f′ (x)在点x的导数称为函数f (x)在点x的二阶导数，记为y″′ =f″′ (x)，即

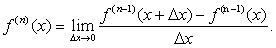
类似地，函数y=f (x)的二阶导数y″′ = f′ ″(x)在点x的导数，称为函数f (x)在点x的三阶导数，记作f' ' ' (x)。一般地，函数y=f (x)的n-1阶导数在点x的导数，称为函数f (x)在点x的n阶导数，记作f(n) (x)，即

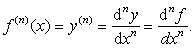
二阶与二阶以上的导数统称为高阶导数。函数y=f (x)在点x的n阶导数记作

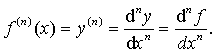
求一个函数的高阶导数，只须反复运用求一阶导数的方法。
由于求高阶导数就是进行一连串的通常的求导运算，而初等函数的导数都是初等函数，所以任何初等函数的任何阶导数仍是初等函数。例如，(a^x)⁽ⁿ⁾＝a^x
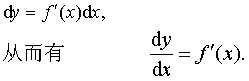
二阶导数有明显的力学意义。若作直线运动的物体的运动规律是s (t)，则物体在时刻t的瞬时速度v(t)= s′ (t)，物体在时刻t的加速度a (t) =s″′ (t)，二阶导数还用于研究曲线的凹凸和拐点。

高阶导数

见“导数”。