单服务台排队模型

---

单位时间的顾客平均到达率和平均服务率为随机型的单服务台排队模型。

它是排队论模型中的基本模型。其假设条件为：(1)输入过程——顾客源是无限的，顾客单个到来，相互独立，一定时间内到达的顾客数服从普阿松分布，输入过程是平稳的。

(2)排队规则——单队，队长没有限制，先到先服务。

(3)服务机构——单服务台，各顾客的服务时间是相互独立的，服从负指数分布。

另外，到达的间隔时间和服务时间也是相互独立。在求解实际的排队问题时，根据实测的数据，确定普阿松分布参数λ和负指数分布参数μ的取值。在上述假设条件下按以下各公式计算系统的各项运行指标：

(1)系统处在繁忙状态的概率(服务强度系数)；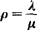

(2)系统处在空闲状态的概率；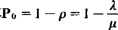

(3)在队列中等待服务的平均顾客数(队列长期望值)L_q

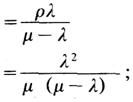
(4)在系统中的平均顾客数(队长期望值)；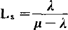

(5)在队列中顾客等待时间

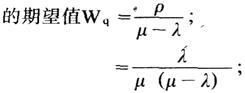
(6)在系统中顾客逗留时间的期望值；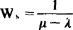

(7)在系统中顾客人数为n的概率P(n)=(1－ρ)ρⁿ

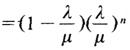
(8)在系统中顾客人数n＞K的概率；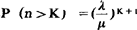

以上指标有如下相互关系：

L_s=λW_s；L_q=λW_q；

；

。

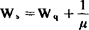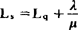根据以上计算的运行指标，就可对系统的运营效率和服务质量，作出评价；并根据管理要求，用解析方法或模拟方法，对提出的设计或改进方案按最小总费用或最大利润原则求得最优解。