卡方(X2)分布

---

小样本推断中最常用的分布。

英国统计学家卡尔·皮尔生(Karl Pearson)提出。设x服从正态分布N(0，1)，又设x₁，x₂，……，x_n为x的一个样本，它们的平方和为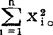。则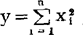服从参数为n的X²分布，其分布密度函数为：

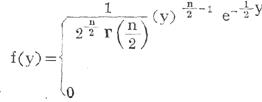
其他

其中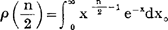卡方分布的数学期望为n，方差为2n。

X²分布上100α百分位点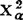(n)是指满足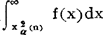=α的点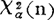。对不同的α及n的100α百分位点有X²表可查。该分布与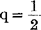，p=n时的r分布相同。

当n很大时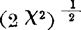近似服从正态分布。

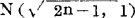X²分布具有可加性，设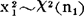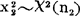，，且它们相互独立，则。

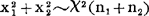X²分布在列联表，方差估计，分布和随机样本参数的假设检验中有著广泛的应用。