卡方(X2)检验

---

统计推断早期方法之一。

英国统计学家皮尔生(Karl Pearson)首创。指基于卡方统计量而进行的显著性检验。它的重要作用：比较落入特定类别的观察次数的适合度检验：比较正态样本的观察方差和理论方差；作为概率组合的检验之用，也可用于分布检验等。

卡方检验基于多项分布，它检验观察值与理论值之间差异的显著性。

设随机变量的取值可分为r组，独立地取n个观察值，n_i为第i组的频数(i=1，2，…，r)，np₁为第i组的理论次数，有：

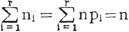
皮尔生证明了统计量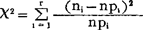的渐近分布是自由度为r－1的X²－分布，故上述统计量X²又称为皮尔生统计量。

当n₁与np₁差异较小时，X²的数值也较小；反之X²的数值就增大，所以它可以检验观察次数与理论次数的一致程度。

给定显著性水平α，从X²－分布表根据自由度r－1可查出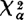。当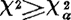时，认为两者之间有显著差异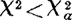；时，则认为两者之间无显著差异。