反三角函数

---

反正弦函数、反余弦函数、反正切函数、反余切函数都叫做反三角函数．

例1 已知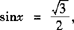，分别在区间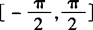，[0，2π]内求方程的解．

分析 当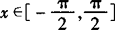时，满足sinx=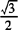的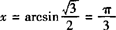；利用诱导公式可知满足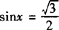且x∈[0，2π]的x有两个值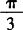与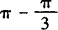；利用终边相同角的三角函数相等可求出实数内的所有解．

解 由y=sinx在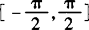上是增函数及反正弦函数的概念知．

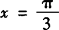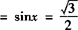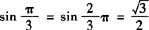当x∈[0，2π]时，由诱导公式sin(π—x)及知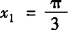，x₂=2/3π．

当x∈R时，据正弦函数的周期性可知x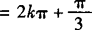或x=2kπ+2/3π(k∈Z)时，sinx=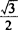．则所求的x的集合是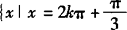或x=2kπ+2/3π，k∈Z}．

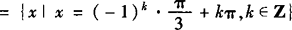评析 对sinx=a，|a|≤1，这个方程的解可表示成x₁=2kπ+arcsina或x₂=2kπ+π—arcsina，从而方程的解集为{x|x=nπ+(—1)ⁿarcsina，n∈Z}．

例2 已知cosx=—3/5，求给定条件下的角x

(1)x∈[0，π]；

(2)x∈[—2π，4π]；

(3)x∈R．

分析 记住arccosx∈[0，π]解法同例1类似．

解 (1)当x∈[0，π]上cosx=—3/5，由反余弦定义，存在惟一的x=arccos(—3/5)(为纯解)

(2)∵x∈[—2π，4π]，角x在坐标平面上转了三周，每一周都有符合条件的两个角，共有6个角，分别是：—π±arccos3/5，π±arccos3/5，³π±arccos3/5．

(3)∵x∈R，满足cosx=—3/5的角x有无数个，它们终边在第二或第三象限，与π±arccos3/5终边相同．

∴x=2kπ+π±arccos3/5(k∈Z)．

评析 对于方程cosx=a，|a|≤1，解集为{x|x=2kπ±arccosa，k∈Z}．

例3 设x₁，x₂是方程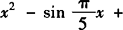 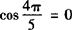的两根，求arctanx₁+arctanx₂之值．