古诺双头垄断模型

---

1838年，法国数理经济学家古诺(A.Cournot)提出的双头垄断厂商的行为模型。

该模型有三个基本假定：(1)双头垄断厂商的产品同质；(2)猜测产量(即一方增加(或减少)产量导致另一方增加(或减少)的产量)的变量为零，即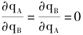，也就是说，双头均假定竞争对手的产量不变；(3)两厂商采取相同的价格。该模型要解决的问题是：(1)双头各自将生产多少产品?(2)市场价格是多少?(3)双头各自的利润是多少?

设A、B为模型中的双头，它们各自面临的需求曲线是共同的市场需求曲线P＝f(q_A+q)_B)，各自的成本函数为：

TC_A＝TC_A(q_A)

TC_B＝TC_B(q_B)

则利润函数分别为：

V_A＝TR_A-TC_A=f(q_A+q_B)·q_A-TC_A

V_B＝TR_B-TC_B=f(q_A+q_B)·q_B-TC_B

可见，每个寡头的利润不仅是本身产量的函数，而且也是竞争对手——另一个寡头产量的函数。

如果A厂商猜测出B厂商的产量为q_B，它就能根据最大化条件进行生产，即：

正是基于反应函数方程组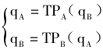的解，即E点所表示的产量组合(q_A，q_B)，双头得以确定各自的产量，并进而确定市场价格及各自的利润数量。

在古诺模型中，两寡头均视对手的反应函数决定自己的最大利润产量，因此，均以对手的既定产量为前提，它们都是对方产量的被动追随者，所以均视对手为领先者。