图解复数法作平面机构的运动分析

---

分析的方法与步骤是：首先作位置分析，画出机构的位置矢量图，由图写出复数形式的位置矢量方程，解方程求未知的位置参数；其次作速度、加速度分析，将一般形式的速度、加速度矢量方程变成复数形式，解复数方程求速度、加速度。

如图5．3-1所示，矢量R可用带箭头的线段表示，也可用复数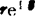表示，即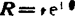，其中v为矢量R的大小；θ为矢量R的方位角，

度量矢量方位角的起始线是由矢量起点向右引出的水平线：由起始线按逆时针方向度量的方位角取“+”值；由起始线按顺时针方向度量的方位角取“-”值。显然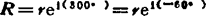，。当r=1时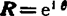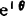，(为单位矢量)。图5．3-2所示为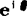圆。可见：

；；。

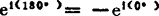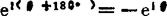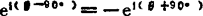在图5．3-3中，a)所示为一平面运动构件。b)表示构件的C点对B点的相对位置矢量BC，即BC=le^1φ(l为B至C的实际长度)。通常规定：角速度ω为逆时针方向时取“+”值，反之取“-”值；角加速度ε为逆时针方向时取“+”值，反之取“-”值。当ω为“+”值时，v_cB的方位角为φ+90°，如图c)所示；当ω为“-”值时，v_CB的方位角为φ-90°。

由于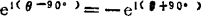，故vCB=lωe^1(φ+90)。同理，==：=；

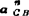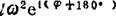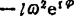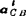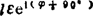相对速度v_B2B1的复数形式：因v_B2B1的方位角为φ或为φ+180°。且v_B2B1往往是待求量，故可假设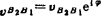。若求得v_B2B1=10m／s，则v_B2B1=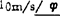；若v_B2B1=-10m／s，则v_B2B1=10m／s。

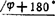哥氏加速度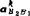的复数形式：因v_B2B1=vB₂B₁e^1φ，故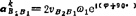。若计算得vB₂B₁ω₁=-5m／s²，显然，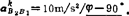

相对加速度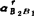的复数形式：可假设=

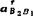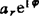
例5．3-15曲柄滑块机构，见图a)。已知l₁=20mm、l₂=60mm、φ₁=60°、ω₁=10rad／s)，求φ₂、S、ω₂、vC、ε₂、aC。