由圆的标准方程展开,得x2+y2—2ax—2by+a2+b2—r2=0,其外形为x2+y2+Dx+Ey+F=0,称为圆的一般方程,配方得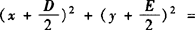
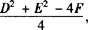 ,其方程式的特点:
,其方程式的特点:
❶ x2,y2项系数相等且不为0;
❷ 没有x·y这样的交叉项.
二元二次方程Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆的充要条件:
若上述的二元二次方程表示圆,则有:A=C≠0,B=0这只是二元二次方程表示圆的必要条件,但不充分.
当A=C≠0,B=0时,上述二次方程可化为: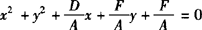 ,此方程表示圆的条件是
,此方程表示圆的条件是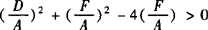 即D2+E2—4AF>0.
即D2+E2—4AF>0.
故有二元二次方程Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆的充要条件是:
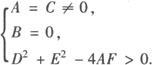
把圆的一般方程x2+y2+Dx+Ey+F=0(D2+E2—4F>0)化为标准方程的一般步骤:
可先把方程左边分别按x,y配方,之后把常数移到右边,即得: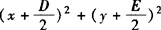
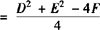 ,进而可得到圆心坐标
,进而可得到圆心坐标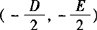 ,半径
,半径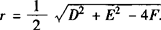 .
.
- 加拿大电影是什么意思
- 加拿大电影委员会是什么意思
- 加拿大电视是什么意思
- 加拿大百科全书是什么意思
- 加拿大的华人与华人社会是什么意思
- 加拿大的月亮是什么意思
- 加拿大皇家银行是什么意思
- 加拿大皇家银行是什么意思
- 加拿大监狱制度是什么意思
- 加拿大短篇小说选是什么意思
- 加拿大社会科学和人文研究理事会成立是什么意思
- 加拿大种子分级标准立法是什么意思
- 加拿大种子品种名称立法是什么意思
- 加拿大种子查封扣押立法是什么意思
- 加拿大种子标牌管理立法是什么意思
- 加拿大种子标签控制立法是什么意思
- 加拿大种子标记标签立法是什么意思
- 加拿大种子检查收费立法是什么意思
- 加拿大种子管理制度立法是什么意思
- 加拿大种子行政执法立法是什么意思
- 加拿大种子进出口立法是什么意思
- 加拿大种子违法处罚立法是什么意思
- 加拿大种薯检验体系立法是什么意思
- 加拿大种薯生产体系立法是什么意思
- 加拿大种薯管理制度立法是什么意思
- 加拿大移民是什么意思
- 加拿大移民政策是什么意思
- 加拿大粮食管理机构立法是什么意思
- 加拿大粮食质量管理立法是什么意思
- 加拿大粮食购销政策立法是什么意思
- 加拿大联合教会是什么意思
- 加拿大联邦实业开发银行是什么意思
- 加拿大联邦议会是什么意思
- 加拿大良种繁育机构立法是什么意思
- 加拿大草坪种子标签立法是什么意思
- 加拿大评议会儿童文学奖是什么意思
- 加拿大豌豆种分级标准立法是什么意思
- 加拿大货币政策是什么意思
- 加拿大贸易法规是什么意思
- 加拿大通讯社是什么意思
- 加拿大野生动物保护立法是什么意思
- 加拿大野生动物咨询委员会立法是什么意思
- 加拿大金融制度是什么意思
- 加拿大金融监管体制是什么意思
- 加拿大铁路华工纪念碑是什么意思
- 加拿大银行是什么意思
- 加拿大银行法是什么意思
- 加拿大风情录是什么意思
- 加拿大高等教育研究学会成立是什么意思
- 加拿大鲁滨孙是什么意思
- 加拿大鲑鱼繁殖保护立法是什么意思
- 加拿大麦种分级标准立法是什么意思
- 加拿大麦种精选规程立法是什么意思
- 加拿大黄江夏总堂是什么意思
- 加捻过程基本理论是什么意思
- 加数←→减数是什么意思
- 加文是什么意思
- 加料佛手散是什么意思
- 加料十全汤是什么意思
- 加料四物汤是什么意思