垂径定理的逆定理

---

平分弦(不是直径)的直径垂直于弦，并且平分弦所对的弧．

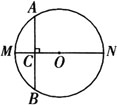
例1 如图☉O中，直径MN垂直于弦AB，垂足为C．

图中相等的线段有＿＿相等的劣弧＿＿．

答 OM=ON

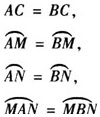
例2 ☉O中，CD为弦，AB为直径，且CD⊥AB，垂足为P，AB=4，PA∶PB=1∶3，求OP和CD的长．

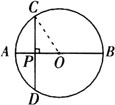
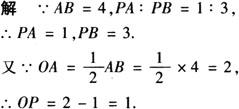
连接OC，在Rt△OCP中，OC=OA=2OP=1，根据勾股定理可得

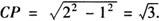
根据垂径定理可知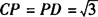，∴CD=2．

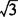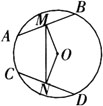
例3 ☉O中，M、N是弦AB、CD的中点，

若∠AMN=∠CNM，

求证：OM=ON．

证明 ∵M为AB中点，O为圆心，

∴OM⊥AB，∴∠OMA=90°．

同理可证∠ONC=90°．

∴∠OMA=∠ONC．

又∵∠AMN=∠CNM，

∴∠OMN=∠ONM．

∴OM=ON．

例4 公路MN和公路PQ在点P处交汇，且∠QPN=30°，点A处有一所中学，AP=160m，假设拖拉机行驶时，周围100m以内会受到噪声的影响，那么拖拉机在公路MN上沿PN方向行驶时，学校是否会受到噪声影响?请说明理由，如果受影响，已知拖拉机的速度为18km/h，那么学校受影响的时间为多少秒?

解 过A点作AB⊥MN于B点．

∵∠QPN=30°，PA=160m．

∴AB=80m<100m．

∴学校会受到噪声影响．

以A为圆心，以100m为半径作☉A与MN交于C、D两点，连接AC，根据勾股定理可得BC=60m．

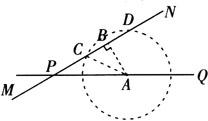
再根据垂径定理可知CD=2BC=120m．

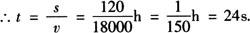
答 学校受影响时间为24s．