声波的分析方法

---

在弹性介质中(包括空气)，某处介质的一部分的振动会带动相邻部分介质相继振动起来，这种振动的传播过程就是声波。

最简单的波是一维的简谐波，如图1所示，设x=0处质点的振动为

u(x=0，t)=Acosωt

该振动依靠弹性沿x轴传播，若传播速度为v，则t时x处的振动情况，应同于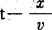时刻x=0处的振动，即：

此即沿x轴传播的一维简谐波的表示式，应注意式中含x表示该式所描述的是一系列质点(处于不同的x处)的有序振动，式中ω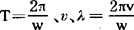，分别称为波的园频率、周期、波速及波长。质点振动的方向(即y的方向)与波的传播方向平行的波称为纵波，质点振动方向与波的传播方向垂直的波称为横波，容易理解，纵波靠介质的纵向弹性(伸长缩短或膨胀压缩)传播，横波靠介质的横向弹性(切变)传播。

一般情况下的波当然不限于简谐波，具体场合下的波是由所谓波方程及附加的初条件及边条件来确定的，作为示例，下面以空气中一维声波为例介绍波方程的导出。

如图2沿x轴方向取截面为s柱状体，考虑(x，x+△x)这一段气体，设不存在波时空气各处的压强为p₀，质量密度为ρ₀，该段空气的质量为psdx，设t时刻x处的位移为u(x，t)，t时刻x+dx处的位移为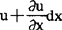，这一小段气体的体积由原来的sdx变成s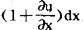。此小段气体左侧所受压力为sp(x+u，t)，右侧所受压力为sp(x+u+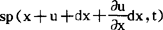，于是根据牛顿运动定律应有