大M法

---

亦称罚因子法。

它是线性规划问题中，当约束条件中加入人工变量以后，为了使问题的解不受引入的人工变量的影响，而采用的一种算法。

M是一个很大的正数，当约束条件引入人工变量以后，若目标函数是极大化(MAX)问题，则引入的人工变量在目标函数中的系数为－M；若目标函数是极小化(Min)问题，则引入的人工变量在目标函数中的系数为+M。

设x_k为引入的人工变量，则

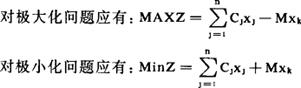
例：MinZ=－3x₁+x₂+x₃

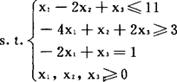
在上述问题的约束条件中加入松弛变量x₄，剩余变量x₅，人工变量X₆，x₇后得到：MinZ=－3x₁+x₂+x₃+Mx₆+Mx₇

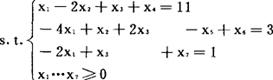
变Min化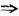MAX化求解：

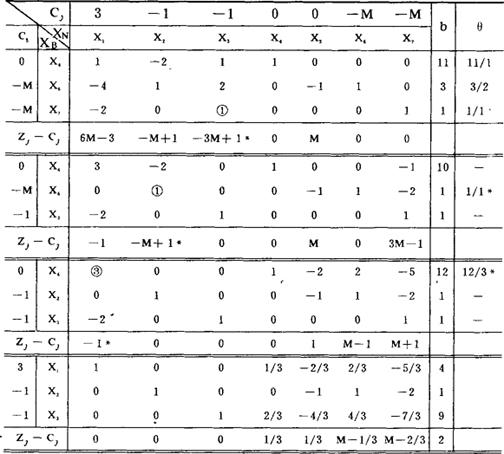
得最优解：x₁^*=4，x₂^*=1，x₃^*=9，

MinZ=－Z=－2