常用的迭代过程终止准则

---

从理论上说，迭代过程可以产生无穷的点列｛X^(k)，k=0，1，2，…｝，直达到目标函数值无限趋近于理论最小值才终止。但在实际中，根据终止准则判断出已取得足够精确的近似最优点时，迭代即可终止。最后所得点即认为是接近理论最优点的近似最优点X*。

不同的最优化方法采用不同的迭代终止准则，但常用的迭代过程终止准则一般有以下几种：

❶ 在迭代过程中，当相邻两次迭代点X^(k)和X^(k+1)的距离已达到小于或等于规定的某一很小的正数ε时，迭代终止。这种迭代终止准则，一般用两个迭代点失量的长度来表示，即

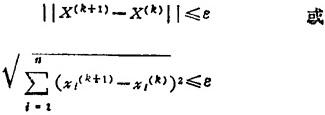
也有用矢量长度在各坐标轴上的分量来表示，即

|X_l^(k+1)－X₁^(k)|≤ε，i=1，2，…，n

❷ 在迭代过程中，当相邻两次迭代点X^(k)和X^(k+1)的目标函数值的下降量已达到小于或等于规定的某一很小的正数ε时，迭代终止。这种迭代终止准则，一般用目标函数值下降量的绝对值或相对值来表示，即

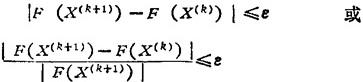
❸ 在迭代过程中，当目标函数在迭代点的梯度达到小于或等于规定的某一很小的正数时，迭代终止。这种迭代终止准则，一般采用梯度矢量的长度来表示，即

‖△F(X^(k))‖≤ε

以上各式中的ε，可根据不同的最优化方法与设计问题对精度的要求而定，随具体的方法和设计问题的不同而异。